Regular language: Difference between revisions

For natural language that is regulated, see List of language regulators.

In theoretical computer science, a regular language is a formal language (i.e., a possibly infinite set of finite sequences of symbols from a finite alphabet) that satisfies the following equivalent properties:

• it can be accepted by a deterministic finite state machine.
• it can be accepted by a nondeterministic finite state machine
• it can be accepted by an alternating finite automaton
• it can be described by a formal regular expression. Note that the "regular expression" features provided with many programming languages are augmented with features that make them capable of recognizing languages which are not regular, and are therefore not strictly equivalent to formal regular expressions.
• it can be generated by a regular grammar
• it can be generated by a prefix grammar
• it can be accepted by a read-only Turing machine
• it can be defined in monadic second-order logic
• it is recognized by some finitely generated monoid
• it is the preimage of a subset of a finite monoid under a homomorphism from the free monoid on its alphabet

Regular languages

The collection of regular languages over an alphabet Σ is defined recursively as follows:

• The empty language Ø is a regular language.
• The empty string language {ε} is a regular language.
• For each a ∈ Σ (a belongs to Σ), the singleton language {a} is a regular language.
• If A and B are regular languages, then A ∪ B (union), A • B (concatenation), and A* (Kleene star) are regular languages.
• No other languages over Σ are regular.

All finite languages are regular. Other typical examples include the language consisting of all strings over the alphabet {a, b} which contain an even number of as, or the language consisting of all strings of the form: several as followed by several bs.

A simple example of a language that is not regular is the set of strings $\{a^{n}b^{n}\,\vert \;n\geq 0\}$. This is because in this language, the number of as controls the number of bs, which is not allowed by any of the above rules.

Complexity results

In computational complexity theory, the complexity class of all regular languages is sometimes referred to as REGULAR or REG and equals DSPACE(O(1)), the decision problems that can be solved in constant space (the space used is independent of the input size). REGULAR ≠ AC⁰, since it (trivially) contains the parity problem of determining whether the number of 1 bits in the input is even or odd and this problem is not in AC⁰. On the other hand, REGULAR does not contain AC⁰, because the nonregular language of palindromes can be recognized in AC⁰.

If a language is not regular, it requires a machine with at least Ω(log log n) space to recognize (where n is the input size). In other words, DSPACE(o(log log n)) equals the class of regular languages. In practice, most nonregular problems are solved by machines taking at least logarithmic space.

Closure properties

The regular languages are closed under the various operations, that is, if the languages K and L are regular, so is the result of the following operations:

• the set theoretic Boolean operations: union $K\cup L$, intersection $K\cap L$, and complement ${\bar {L}}$. From this also difference $K-L$ follows.
• the regular operations: union $K\cup L$, concatenation $K\circ L$, and Kleene star $L^{*}$.
• the trio operations: string homomorphism, inverse string homomorphism, and intersection with regular languages. As a consequence they are closed under arbitrary finite state transductions, like quotient $K/L$ with a regular language. Even more, regular languages are closed under quotients with arbitrary languages: If L is regular then L/K is regular for any K.
• the reverse (or mirror image) $L^{R}$.

Deciding whether a language is regular

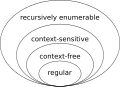
To locate the regular languages in the Chomsky hierarchy, one notices that every regular language is context-free. The converse is not true: for example the language consisting of all strings having the same number of a's as b's is context-free but not regular. To prove that a language such as this is not regular, one uses the Myhill–Nerode theorem or the pumping lemma.

• 
  Regular language in classes of Chomsky hierarchy. "Regular => context free" and not reverse can be observed directly from this picture.

There are two purely algebraic approaches to define regular languages. If:

• Σ is a finite alphabet,
• Σ* denotes the free monoid over Σ consisting of all strings over Σ,
• f : Σ* → M is a monoid homomorphism where M is a finite monoid,
• S is a subset of M

then the set $\{w\in \Sigma ^{*}\,|\,f(w)\in S\}$ is regular. Every regular language arises in this fashion.

If L is any subset of Σ*, one defines an equivalence relation ~ (called the syntactic relation) on Σ* as follows: u ~ v is defined to mean

uw ∈ L if and only if vw ∈ L for all w ∈ Σ*

The language L is regular if and only if the number of equivalence classes of ~ is finite (A proof of this is provided in the article on the syntactic monoid). When a language is regular, then the number of equivalence classes is equal to the number of states of the minimal deterministic finite automaton accepting L.

A similar set of statements can be formulated for a monoid $M\subset \Sigma ^{*}$. In this case, equivalence over M leads to the concept of a recognizable language.

Finite languages

A specific subset within the class of regular languages is the finite languages – those containing only a finite number of words. These are regular languages, as one can create a regular expression that is the union of every word in the language.

The number of words in a regular language

For any regular language $L$ there exist constants $\lambda _{1},\,\ldots ,\,\lambda _{k}$ and polynomials $p_{1}(x),\,\ldots ,\,p_{k}(x)$ such that for every $n$ the number $s_{L}(n)$ of words of length $n$ in $L$ satisfies the equation $s_{L}(n)=p_{1}(n)\lambda _{1}^{n}+\dotsb +p_{k}(n)\lambda _{k}^{n}$. Thus, a non-regularity of some language $L'$ can be proved by counting the words in $L'$. Consider, for example, the Dyck language of strings of balanced parentheses. The number of words of length $2n$ in the Dyck language is equal to the Catalan number $C_{n}\sim {\frac {4^{n}}{n^{3/2}{\sqrt {\pi }}}}$, which is not of the form $p(n)\lambda ^{n}$, witnessing the non-regularity of the Dyck language.

See also

• Pumping lemma for regular languages
• Union of two regular languages

References

• Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 0-534-94728-X. Chapter 1: Regular Languages, pp.31–90. Subsection "Decidable Problems Concerning Regular Languages" of section 4.1: Decidable Languages, pp.152–155.

External links

• Complexity Zoo: Class REG