في الرياضيات ، متسلسلة (بالإنجليزية : Convergent series ) هي مجموع حدود متتالية من الأعداد.[ 1] [ 2]
لتكن
{
a
1
,
a
2
,
a
3
,
…
}
{\displaystyle \left\{a_{1},\ a_{2},\ a_{3},\dots \right\}}
للمجموع الجزئي
S
n
{\displaystyle S_{n}}
S
n
=
∑
k
=
1
n
a
k
.
{\displaystyle S_{n}=\sum _{k=1}^{n}a_{k}.}
تكون متسلسلة ما متقاربة إذا كانت متتالية المجاميع الجزئية
{
S
1
,
S
2
,
S
3
,
…
}
{\displaystyle \left\{S_{1},\ S_{2},\ S_{3},\dots \right\}}
نهاية
ℓ
{\displaystyle \ell }
ε
>
0
{\displaystyle \varepsilon >0}
N
{\displaystyle N}
n
≥
N
{\displaystyle n\geq \ N}
|
S
n
−
ℓ
|
≤
ε
.
{\displaystyle \left|S_{n}-\ell \right\vert \leq \ \varepsilon .}
يقال عن متسلسلة غير متقاربة متسلسلة متباعدة .
مجموع مقلوبات الأعداد الطبيعية يعطي متسلسلة متباعدة تسمى المتسلسلة المتناسقة :
1
1
+
1
2
+
1
3
+
1
4
+
1
5
+
1
6
+
⋯
→
∞
.
{\displaystyle {1 \over 1}+{1 \over 2}+{1 \over 3}+{1 \over 4}+{1 \over 5}+{1 \over 6}+\cdots \rightarrow \infty .}
مجموع مقلوبات الأعداد الطبيعية مع جعل إشارتها تتناوب بين السالب والموجب، يعطي متسلسة متقاربة:
1
1
−
1
2
+
1
3
−
1
4
+
1
5
⋯
=
ln
(
2
)
{\displaystyle {1 \over 1}-{1 \over 2}+{1 \over 3}-{1 \over 4}+{1 \over 5}\cdots =\ln(2)}
مجموع مقلوبات الأعداد الطبيعية الفردية مع جعل إشارتها تتناوب بين السالب والموجب (صيغة لايبنتس ل π ), يعطي متسلسة متقاربة:
1
1
−
1
3
+
1
5
−
1
7
+
1
9
−
1
11
+
⋯
=
π
4
.
{\displaystyle {1 \over 1}-{1 \over 3}+{1 \over 5}-{1 \over 7}+{1 \over 9}-{1 \over 11}+\cdots ={\pi \over 4}.}
مجموع مقلوبات الأعداد الأولية يعطي متسلسة متباعدة (هذا برهان على أن عدد الأعداد الأولية غير منته):
1
2
+
1
3
+
1
5
+
1
7
+
1
11
+
1
13
+
⋯
→
∞
.
{\displaystyle {1 \over 2}+{1 \over 3}+{1 \over 5}+{1 \over 7}+{1 \over 11}+{1 \over 13}+\cdots \rightarrow \infty .}
مجموع مقلوبات الأعداد المثلثية يعطي متسلسلة متقاربة:
1
1
+
1
3
+
1
6
+
1
10
+
1
15
+
1
21
+
⋯
=
2.
{\displaystyle {1 \over 1}+{1 \over 3}+{1 \over 6}+{1 \over 10}+{1 \over 15}+{1 \over 21}+\cdots =2.}
مجموع مقلوبات عاملي الأعداد الطبيعية يعطي متسلسلة متقاربة (انظر إلى العدد e ):
1
1
+
1
1
+
1
2
+
1
6
+
1
24
+
1
120
+
⋯
=
e
.
{\displaystyle {\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{6}}+{\frac {1}{24}}+{\frac {1}{120}}+\cdots =e.}
مجموع مقلوبات المربعات الكاملة يعطي متسلسلة متقاربة (انظر إلى معضلة بازل ):
1
1
+
1
4
+
1
9
+
1
16
+
1
25
+
1
36
+
⋯
=
π
2
6
.
{\displaystyle {1 \over 1}+{1 \over 4}+{1 \over 9}+{1 \over 16}+{1 \over 25}+{1 \over 36}+\cdots ={\pi ^{2} \over 6}.}
مجموع مقلوبات قوى العدد اثنين يعطي متسلسلة متقاربة:
1
1
+
1
2
+
1
4
+
1
8
+
1
16
+
1
32
+
⋯
=
2.
{\displaystyle {1 \over 1}+{1 \over 2}+{1 \over 4}+{1 \over 8}+{1 \over 16}+{1 \over 32}+\cdots =2.}
مجموع مقلوبات قوى العدد اثنين مع جعل إشارتها تتناوب بين السالب والموجب، يعطي أيضا متسلسلة متقاربة:
1
1
−
1
2
+
1
4
−
1
8
+
1
16
−
1
32
+
⋯
=
2
3
.
{\displaystyle {1 \over 1}-{1 \over 2}+{1 \over 4}-{1 \over 8}+{1 \over 16}-{1 \over 32}+\cdots ={2 \over 3}.}
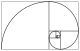
مجموع مقلوبات أعداد فيبوناتشي يعطي متسلسلة متقاربة (انظر إلى العدد ψ ):
1
1
+
1
1
+
1
2
+
1
3
+
1
5
+
1
8
+
⋯
=
ψ
.
{\displaystyle {\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{8}}+\cdots =\psi .}
إذا بُرهن على أن المتسلسلة الزرقاء
Σ
b
n
{\displaystyle \Sigma b_{n}}
Σ
a
n
{\displaystyle \Sigma a_{n}}
Σ
a
n
{\displaystyle \Sigma a_{n}}
Σ
b
n
{\displaystyle \Sigma b_{n}}
هناك عدة طرق تمكن من معرفة هل متسلسلة ما تتقارب أو تتباعد.
اختبار المقارنة
{
a
n
}
{\displaystyle \left\{a_{n}\right\}}
{
b
n
}
{\displaystyle \left\{b_{n}\right\}}
n :
0
≤
a
n
≤
b
n
{\displaystyle 0\leq \ a_{n}\leq \ b_{n}}
∑
n
=
1
∞
b
n
{\displaystyle \sum _{n=1}^{\infty }b_{n}}
∑
n
=
1
∞
a
n
.
{\displaystyle \sum _{n=1}^{\infty }a_{n}.}
وبشكل مماثل، إذا توفر ما يلي مهما كانت قيمة n:
0
≤
a
n
≤
b
n
{\displaystyle 0\leq \ a_{n}\leq \ b_{n}}
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
∑
n
=
1
∞
b
n
{\displaystyle \sum _{n=1}^{\infty }b_{n}}
اختبار النسبة
a
n
>
0
{\displaystyle a_{n}>0}
r
{\displaystyle r}
lim
n
→
∞
a
n
+
1
a
n
=
r
.
{\displaystyle \lim _{n\to \infty }{\frac {a_{n+1}}{a_{n}}}=r.}
إذا كان r <1, فإن المتسلسلة متقاربة. وإذا كان r > 1,r = 1,
اختبار الجذر أو الجذر النوني
اختبار التكامل
اختبار مقارنة النهايات
اختبار المتسلسلات المتناونة الإشارة