Minimax
En teoria de jocs, Minimax és un mètode de decisió per minimitzar la pèrdua màxima de la imatge esperada en jocs amb adversari i amb informació perfecta. Minimax és un algorisme recursiu.
El funcionament de Minimax es pot resumir com triar el millor moviment per a tu mateix suposant que el teu contrincant escollirà el pitjor per a tu.
Història
Encara que existeixen evidències que Charles Babbage ja havia treballat abans sobre una idea similar,[1] va ser el matemàtic francès Émile Borel el primer a oferir el 1921 un tractament rigorós als jocs competitius i en estudiar les estratègies aplicables als jocs de suma zero.[2][3] No obstant això sol atribuir-se a John von Neumann el principal mèrit de la concepció del principi minimax, ja que va ser ell qui, en el seu article de 1928 Zur Theorie der Gesellschaftsspiele (Sobre la teoria dels jocs de societat) publicat a la revista Mathematische Annalen,[4] va posar les bases de la moderna teoria de jocs i va provar el teorema fonamental del minimax, pel qual es demostra que per a jocs de suma zero amb informació perfecta entre dos competidors existeix una única solució òptima.[5]
Teorema Minimax
John von Neumann és el creador del teorema minimax, que va donar la següent noció del que era un joc:
"Un joc és una situació conflictiva en la qual un ha de prendre una decisió sabent que els altres també prenen decisions, i que el resultat del conflicte es determina, d'alguna manera, a partir de totes les decisions realitzades. "
També va afirmar que:
"Sempre hi ha una manera racional d'actuar en jocs de dos participants, si els interessos que els governen són completament oposats. "
La demostració a aquesta afirmació es diu Teoria Minimax i sorgeix el 1926.
Aquest teorema estableix que en els jocs bipersonal de suma nul, on cada jugador coneix per endavant l'estratègia del seu oponent i les seves conseqüències, hi ha una estratègia que permet a tots dos jugadors minimitzar la pèrdua màxima esperada. En particular, quan s'examina cada possible estratègia, un jugador ha de considerar totes les respostes possibles del jugador adversari i la pèrdua màxima que pot comportar. El jugador juga, doncs, amb l'estratègia que resulta en la minimització de la seva màxima pèrdua. Tal estratègia és anomenada òptima per a tots dos jugadors només en cas que les seves Minimax siguin iguals (en valor absolut) i contraris (en signe). Si el valor comú és zero el joc es converteix en un sense sentit.
Algorisme Minimax amb moviments alternatius
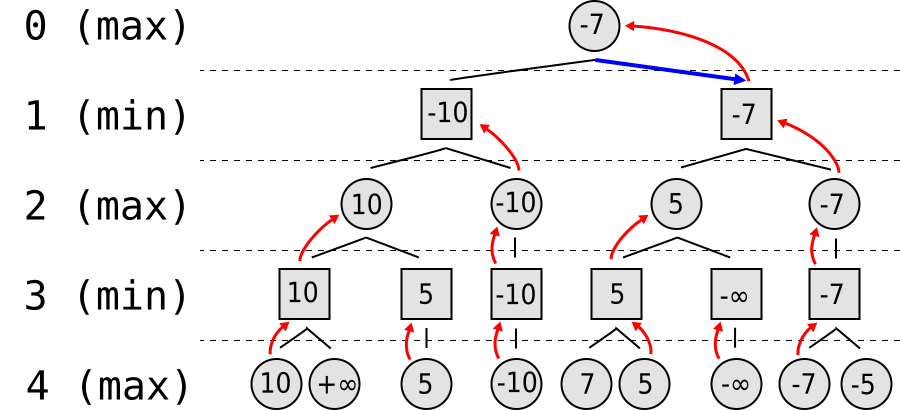 Passos de l'algorisme Minimax:
Passos de l'algorisme Minimax:
- Generació de l'arbre de joc. Es generaran tots els nodes fins a arribar a un estat terminal.
- Càlcul dels valors de la funció d'utilitat per a cada node terminal.
- Calcular el valor dels nodes superiors a partir del valor dels inferiors. Alternativament s'elegiran els valors mínims i màxims representant els moviments del jugador i de l'oponent, d'aquí el nom de Minimax.
- Escollir la jugada valorant els valors que han arribat al nivell superior.
L'algorisme explora els nodes de l'arbre assignant un valor numèric mitjançant una funció d'avaluació, començant pels nodes terminals i pujant cap a l'arrel. La funció d'utilitat defineix com és de bona la posició per a un jugador quan hi arriba. En el cas dels escacs els possibles valors són (+1,0, -1) que es corresponen amb guanyar, empatar i perdre respectivament. En el cas del backgammon els possibles valors tenen un rang de [+192, -192], que corresponen amb el valor de les fitxes. Per a cada joc poden ser diferents.
Si Minimax s'enfronta amb el dilema del presoner, escull sempre l'opció amb la qual maximitza el seu resultat suposant que el contrincant intenta minimitzar-lo.
Exemple
En el següent exemple es pot veure el funcionament de Minimax en un arbre generat per un joc imaginari. Els possibles valors de la funció d'utilitat tenen un rang de [1-9]. En els moviments del contrincant suposem que escollirà els moviments que minimitzin la nostra utilitat, en els nostres moviments suposem que escollirem els moviments que maximitzen la nostra utilitat.
El primer pas serà calcular els nodes terminals, en verd. Posteriorment calcularem el quart nivell, moviment min, minimitzant el triat (5, 2 i 1). Després podrem calcular el tercer nivell, moviment màx, maximitzant la utilitat (5, 9). El segon nivell és un moviment mín (5, 3 i 1). Finalment arribem al primer nivell, el moviment actual, triarem el node que maximitzi la nostra utilitat (5).
Optimització
En la pràctica el mètode Minimax és impracticable excepte en supòsits senzills. Realitzar la recerca completa requeririen quantitats excessives de temps i memòria.
Claude Shannon en el seu text sobre escacs de 1950 ( Programming a Computer for Playing Chess ) va proposar limitar la profunditat de la recerca en l'arbre de possibilitats i determinar el seu valor mitjançant una funció heurística. Per optimitzar Minimax pot limitar la recerca per nivell de profunditat o per temps d'execució. Una altra possible tècnica és l'ús de la poda alfa-beta. Aquesta optimització es basa en la suposició que el jugador contrari no ens permetrà jugar les nostres millors jugades.
Referències
- ↑ Beal, 1999, p. 2.
- ↑ Borel, 1921.
- ↑ Mosterín, 2000, p. 210.
- ↑ Neumann, 1928.
- ↑ Mosterín, 2000, p. 210-211.
Bibliografia
- Beal, Donald F. The Nature of Minimax Search. Universidad de Maastricht: Institute of Knowledge and Agent Technology, UM, 1999.
- «La theorie du jeu et les equations integrales ä noyau symetrique». Comptes rendus de l'Académie des sciences, 1921.
- Herik, Jaap van. Computerschaak, Schaakwereld en Kunstmatige Intelligentie. La Haya: Delft University of Technology. Academic Service, 1983.
- Mosterín, Jesús. Los lógicos. Madrid: Espasa Calpe, 2000.
- Wiener, Norbert. Cybernetics: Or Control and Communication in the Animal and the Machine. Cambridge: MIT Press, 1948.

