Z Wikipedie, otevřené encyklopedie
Kosinus je goniometrická funkce . V pravoúhlém trojúhelníku bývá definována jako poměr přilehlé odvěsny a přepony. Pro označení této funkce se obvykle používá zkratka cos a jejím grafem je kosinusoida . Definuje se buď na oboru reálných čísel anebo jako komplexní funkce komplexní proměnné.
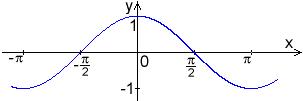
Graf funkce kosinus.
Funkce
y
=
cos
x
{\displaystyle y=\cos x\,\!}
k je libovolné celé číslo ):
Definiční obor
R
{\displaystyle \mathbb {R} }
reálná čísla )Obor hodnot
⟨
−
1
;
1
⟩
{\displaystyle \langle -1;1\rangle }
Rostoucí
(
π
+
2
k
π
,
2
π
+
2
k
π
)
{\displaystyle \left(\pi +2k\pi ,2\pi +2k\pi \right)}
Klesající
(
2
k
π
,
π
+
2
k
π
)
{\displaystyle \left(2k\pi ,\pi +2k\pi \right)}
Maximum
2
k
π
{\displaystyle 2k\pi }
Minimum
π
+
2
k
π
{\displaystyle \pi +2k\pi }
Derivace
y
′
=
−
sin
x
{\displaystyle y'=-\sin x\,\!}
Integrál
∫
cos
x
d
x
=
sin
x
+
c
{\displaystyle \int \cos x\,\mathrm {d} x=\sin x+c}
Taylorův polynom
cos
x
=
1
−
x
2
2
!
+
x
4
4
!
−
x
6
6
!
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
x
2
n
(
2
n
)
!
{\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}}
Inverzní funkce arkus kosinus (arccos )je:
Funkce kosinus je v komplexních číslech definována součtem řady
cos
z
=
1
−
z
2
2
!
+
z
4
4
!
−
z
6
6
!
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
z
2
n
(
2
n
)
!
{\displaystyle \cos z=1-{\frac {z^{2}}{2!}}+{\frac {z^{4}}{4!}}-{\frac {z^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n}}{(2n)!}}}
která konverguje na celé komplexní rovině . Pro každá dvě komplexní čísla z 1 ,z 2 platí:
cos
z
=
e
i
z
+
e
−
i
z
2
,
{\displaystyle \cos z={\frac {e^{iz}+e^{-iz}}{2}},}
cos
(
z
1
+
z
2
)
=
cos
z
1
cos
z
2
−
sin
z
1
sin
z
2
,
{\displaystyle \cos \left(z_{1}+z_{2}\right)=\cos z_{1}\cos z_{2}-\sin z_{1}\sin z_{2},}
cos
i
z
=
cosh
z
,
{\displaystyle \cos iz=\cosh z,\,}
Tyto vzorce plynou přímo z příslušných definičních mocninných řad daných funkcí . Kosinus je na celé komplexní rovině jednoznačná holomorfní funkce.