Axiom výběru

Diagram axiomu výběru

Axiom výběru (ozn. AC z angl. axiom of choice) je axiom často přidávaný k obvyklým axiomům Zermelovy–Fraenkelovy teorie množin (ZF). Poprvé jej formuloval Ernst Zermelo v roce 1904.

Jde o tvrzení z lidského pohledu samozřejmé (zjevně platné), ale přesto nedokazatelné - ovšem ani nevyvratitelné - ze Zermelo–Fraenkelových axiomů nebo jiných běžných axiomatizací.

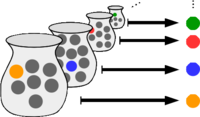
Axiom tvrdí, že ke každé množině neprázdných množin $N$, například $\{\{1\},\{2,3\},\{1,3,5\}\}$ existuje selektor, tj. zobrazení, který každé množině $a\in N$ přiřadí nějaký její prvek $x\in a$. V uvedeném případě existuje šest takových selektorů, například takový, který množině $\{1\}$ přiřadí jedničku, množině $\{2,3\}$ např. trojku a množině $\{1,3,5\}$ např. také trojku.

Axiom výběru zní: Každá množina neprázdných množin má selektor.

U přirozených čísel je existence selektoru snadno dokazatelná i bez axiomu výběru: jedna z mnoha možností je přiřadit každé množině přirozených čísel nejmenší z nich. Ovšem na reálných číslech taková možnost není k dispozici: zkonstruovat zobrazení, které každé neprázdné množině reálných čísel přiřadí některý její prvek, je nemožné bez velmi silných dodatečných axiomů, jako např. axiom konstruovatelnosti. Ten je mnohem silnější než axiom výběru (který z něj plyne), tvrdí toho více a mnohem výrazněji omezuje možnosti, jak může vypadat univerzum všech množin.

Axiom výběru tvrdí, že takový selektor existuje na reálných číslech či na libovolné množině, aniž by - na rozdíl od axiomu konstruovatelnosti - podával návod, jak takové zobrazení vytvořit nebo jak vypadá. Toto je hlavní námitka proti němu. Lze díky němu sice sestrojit významné matematické objekty a protipříklady (existenci lebesgueovsky neměřitelné množiny, nebo viz Banachův–Tarského paradox), ovšem bez jakékoli informace, jak vlastně vypadají. Axiom říká, že existuje nějaký selektor, z toho lze dokázat, že existuje nějaká neměřitelná množina.

Přesto se axiom výběru běžně akceptuje, na rozdíl od všech ostatních dodatečných axiomů, jako je Hypotéza kontinua či její negace, nebo např. existence některých velkých kardinálních čísel. Jinými slovy, ZFC (Zermelo–Fraenkelovy axiomy plus axiom výběru) je standardně akceptovaná teorie, která definuje matematickou pravdu, tj. to, co v matematice platí.

Bez axiomu výběru totiž nelze dokázat řadu tvrzení, která jsou nejen intuitivně samozřejmá, ale zároveň jsou v podstatě nutná k budování matematiky. Nelze bez něho dokázat např. ekvivalenci dvou možných definic spojitosti funkce $f:\mathbb {R} \rightarrow \mathbb {R}$ v bodě $x_{0}$: Je-li nespojitá v „epsilon-delta“ smyslu, pak existuje $\varepsilon >0$ tak, že množina $X=\{x\in \mathbb {R} ,|f(x)-f(x_{0})|\geq \varepsilon \}$ má průnik s každým $\delta$-okolí bodu $x_{0}$. Bez axiomu výběru není možné - ač se to intuitivně zdá samozřejmé - prohlásit, že existuje posloupnost $a_{n}$ taková, že $a_{1}$ je některý z prvků $X$ z $1$-okolí (tj. pro $\delta =1$) bodu $x_{0}$, za $a_{2}$ libovolný z $1/2$-okolí, za $n$-tý vzít libovolný prvek $X$ z ${\frac {1}{n}}$-okolí bodu $x_{0}$ atd. Sice pro každé $n\in \mathbb {N}$ nějaký existuje, ovšem bez axiomu výběru nelze prohlásit, že „stačí vzít libovolný z nich“. Taková posloupnost existovat nemusí a bylo dokázáno, že některých světech matematiky (tj. modelech ZF) skutečně neexistuje.

Axiom výběru je ekvivalentní s mnoha dalším tvrzeními - každé z nich platí, právě když platí axiom výběru. Příkladem je Zermelova věta tvrdící, že na každé množině existuje nějaké dobré uspořádání; to zásadně usnadňuje porovnávání velikostí množin pomocí kardinálních čísel.

Formulace

Tento axiom tvrdí:

Pro každý neprázdný soubor neprázdných množin existuje funkce, která z každé množiny tohoto souboru vybírá právě jeden prvek.

V matematické notaci:

$(\forall I\neq \emptyset )(\forall i)(i\in I\implies A_{i}\neq \emptyset )\implies (\exists f(f\ {\mbox{je funkce}}\,\land \,\operatorname {dom} (f)=I\,\land \,(\forall i)(i\in I\implies f(i)\in A_{i})))$.

Motivace pro přijetí AC

Důležitou vlastností AC je to, že umožňuje ke každému souboru množin získat soubor jejich prvků, z každé množiny jeden, a to bez znalosti jakéhokoli algoritmu, kterým by tento výběr prvků mohl být proveden, pouze z předpokladu neprázdnosti souboru i jednotlivých množin (tj. nekonstruktivně). Na konečném souboru množin je AC snadno dokazatelný – i podle selského rozumu je zřejmé, že vybrat z každé hromady kamení jeden kámen není žádný problém. Problémem začíná být až nekonečný soubor množin, a to především soubory „hodně nekonečné“ (nespočetné, bez dobrého uspořádání).

V některých odvětvích matematiky, zejména v nekonečné kombinatorice, ale například i v matematické analýze, se AC ukazuje jako zcela nezbytný předpoklad pro rozvoj těchto disciplín. S AC je ekvivalentní řada principů teorie množin, které zásadním způsobem „učesávají“ svět teorie množin – nejznámějšími z nich jsou princip maximality a princip dobrého uspořádání. Přijetím axiomu výběru se tedy svět teorie množin stává (z pohledu jeho příznivců) přehlednějším, ale ne zas tolik, aby přestal být zajímavým.

Motivace pro odmítnutí AC

Odpůrci zařazení AC mezi standardní axiomy teorie množin (například konstruktivisté) poukazují na jeho odlišný charakter od ostatních podobných axiomů teorie množin, které obvykle postulují možnost vytvoření nové množiny z již existujících množin jednoduchým a přehledným způsobem (viz axiom sumy, axiom potence, axiom dvojice). Na rozdíl od nich AC nedává žádnou představu o tom, jak výběrová funkce (viz formulace axiomu) vypadá – je tedy spíše „čistě existenční“ než „konstrukční“.

Druhým argumentem je, že AC příliš omezuje rozmanitost objektů ve světě teorie množin – podle principu dobrého uspořádání ekvivalentního s AC lze každou množinu uspořádat tak, aby byla izomorfní s některým ordinálním číslem – to tvrzení tak vlastně říká, že teorie množin nepopisuje žádné objekty, které by nešlo dobře uspořádat.

Dalo by se říci, že svět ZF s AC stojí někde na půli cesty mezi rozmanitým, ale hůře popsatelným a použitelným světem ZF bez AC, a mezi příliš omezeným a zjednodušeným, ale zato dokonale přehledným světem ZF s axiomem konstruovatelnosti.

Nezávislost AC na axiomech ZF

AC je bezesporný neboli konzistentní s ostatními axiomy Zermelovy-Fraenkelovy teorie množin (je takzvaně relativně bezesporný s ZF). Platí totiž v jednom modelu teorie množin, a to v univerzu konstruovatelných množin, což dokázal v roce 1940 Kurt Gödel. V tomto modelu platí dokonce axiom silného výběru a dále například zobecněná hypotéza kontinua.

Také negace AC je relativně bezesporná s ZF, a tedy AC je nezávislý na axiomech ZF. Přidáním negace AC k ZF však vzniká již teorie s dosti podivnými vlastnostmi (lze v ní například bezesporně předpokládat neplatnost klasické Heineho věty).

Související články

• Zermelova-Fraenkelova teorie množin
• Hypotéza kontinua
• Konstruovatelná množina
• Axiom silného výběru
• Axiom úplného výběru
• Axiom závislého výběru
• Axiom spočetného výběru

Externí odkazy

• Obrázky, zvuky či videa k tématu Axiom výběru na Wikimedia Commons

Autoritní data	GND: 4143673-8 LCCN: sh85010586 NDL: 00570783 NLI: 987007282446705171

Portály: Matematika