Cryptographic hash function

In cryptography, a cryptographic hash function is a hash function with certain additional security properties to make it suitable for use as a primitive in various information security applications, such as authentication and message integrity. A hash function takes a long string (or message) of any length as input and produces a fixed length string as output, sometimes termed a message digest or a digital fingerprint.

Overview

Broadly speaking, the security properties are required to ensure that the digest is "random" to prospective attackers, and does not leak any other information about the message itself, and that other messages cannot be found that produce the same digest. Any change to the message, even a single bit, should result in a dramatically different message digest when re-generated from the received message. A cryptographic hash function is considered insecure if either of the following is computationally feasible:

finding a (previously unseen) message that matches a given digest
finding "collisions", wherein two different messages have the same message digest.

An attacker who can do either of these things might, for example, use them to substitute an unauthorized message for an authorized one.

Related algorithms

Checksums and Cyclic redundancy checks (CRCs) are quite distinct from cryptographic hash functions, and are used for different applications. If used for security, they are vulnerable to attack; for example, a CRC was used for message integrity in the WEP encryption standard, but an attack was readily discovered which exploited the linearity of the checksum specified.

A message authentication code or MAC takes a message and a secret key and generates a "MAC tag", such that it is difficult for an attacker to generate a valid (message, tag) pair that doesn't mach one they've already seen; they are used to prevent attackers forging messages, among other uses. Though it is sometimes referred to as a "keyed hash function", a MAC serves a very different purpose and has very different security properties than a cryptographic hash function; for example, it is not considered a flaw if it is easy for someone who knows the MAC key to generate two messages that have the same MAC. Hash functions can be used to create MAC functions; see for example HMAC.

Cryptographic properties

There is no formal definition which captures all of the properties considered desirable for a cryptographic hash function. However, the properties below are generally considered prerequisites:

Preimage resistant (See one way for a related but slightly different property): given h it should be hard to find m such that h = hash(m).
Second preimage resistant: given an input m₁, it should be hard to find another input, m₂ (not equal to m₁) such that hash(m₁) = hash(m₂).
Collision-resistant: it should be hard to find two different messages m₁ and m₂ such that hash(m₁) = hash(m₂). Because of the birthday paradox this means the hash function must have a larger image than is required for preimage-resistance.

A hash function meeting these criteria may still have undesirable properties. For instance, most popular hash functions are vulnerable to length-extension attacks: given h(m) and len(m) but not m, by choosing a suitable m' an attacker can calculate h(m + m'), where + denotes concatenation. This property can be used to break naive authentication schemes based on hash functions. The HMAC construction works around these problems.

The strongest assumption that can be made about the goodness of a hash function is the random oracle model. In fact, this assumption is so strong that no real hash function can meet it.

Applications of hash functions

A typical use of a cryptographic hash would be as follows: Alice poses to Bob a tough math problem and claims she has solved it. Bob would like to try it himself, but would yet like to be sure that Alice is not bluffing. Therefore, Alice writes down her solution, appends a random nonce, computes its hash and tells Bob the hash value (whilst keeping the solution secret). This way, when Bob comes up with the solution himself a few days later, Alice can verify his solution but still be able to prove that she had the solution earlier.

In actual practice, Alice and Bob will often be computer programs, and the secret would be something less easily spoofed than a claimed puzzle solution. The above application is called a commitment scheme. Another important application of secure hashes is verification of message integrity. Determination of whether or not any changes have been made to a message (or a file), for example, can be accomplished by comparing message digests calculated before, and after, transmission (or any other event) (see Tripwire, a system using this property as a defense against malware and malfeasance). A message digest can also serve as a means of reliably identifying a file. A related application is password verification. Passwords are usually not stored in cleartext, for obvious reasons, but instead in digest form. To authenticate a user, the password presented by the user is hashed and compared with the stored hash.

For both security and performance reasons, most digital signature algorithms specify that only the digest of the message be "signed", not the entire message. Hash functions can also be used in the generation of pseudorandom bits.

SHA-1, MD5, and RIPEMD-160 are among the most commonly-used message digest algorithms as of 2004. In August 2004, researchers found weaknesses in a number of hash functions, including MD5, SHA-0 and RIPEMD. This has called into question the long-term security of later algorithms which are derived from these hash functions. In particular, SHA-1 (a strengthened version of SHA-0), RIPEMD-128 and RIPEMD-160 (strengthened versions of RIPEMD). Neither SHA-0 nor RIPEMD are widely used since they were replaced by their strengthened versions.

Hashes are used to identify files on peer-to-peer filesharing networks. For example, in a ed2k link the hash is combined with the filename and the file size, providing sufficient information for locating file sources, downloading the file and verifying its contents.

Iterated hash functions

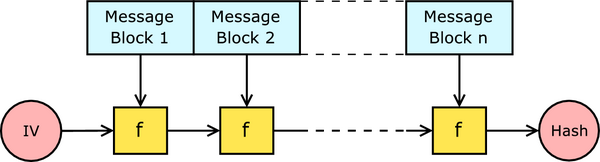
A hash function must be able to process an arbitrary-length message into a fixed-length output. In practice, this can be achieved by breaking the input up into a series of equal-size blocks, and operating on them in sequence using a compression function. This design is known as an iterated hash function, or alternatively, the Merkle-Damgård structure; most widely-used hash functions take this form:

In the diagram, the compression function is denoted by f, and transforms a fixed-length input to an output of the same size. The algorithm starts with an initial value, the initialisation vector (IV). For each message block, the compression function f takes the result so far, combines it with the block, and produces an intermediate result. Crucially, bits representing the length of the entire message are appended to the message and padded suitably as part of the last block. The value after the last block is taken to be the hash value for the entire message.

The popularity of this construction is due to the fact, proved by Merkle and Damgård, that if the compression function f is collision-resistant, then so is the hash function constructed using it.

List of cryptographic hash functions

External links

The Hash function lounge — a list of hash functions and known attacks
A collection of links on the topic
Diagrams explaining cryptographic hash functions
An Illustrated Guide to Cryptographic Hashes by Steve Friedl
Cryptanalysis of MD5 and SHA: Time for a New Standard by Bruce Schneier