Anchor modeling

Anchor modeling is an agile database modeling technique suited for information that changes over time both in structure and content. It provides a graphical notation used for conceptual modeling similar to that of entity-relationship modeling, with extensions for working with temporal data. The modeling technique involves four modeling constructs: the anchor, attribute, tie and knot, each capturing different aspects of the domain being modeled.[1] The resulting models can be translated to physical database designs using formalized rules. When such a translation is done the tables in the relational database will mostly be in the sixth normal form.
Philosophy
Anchor modeling was created in order to take advantage of the benefits from a high degree of normalization while avoiding its drawbacks which higher normal forms have with regards to human readability. Advantages such as being able to non-destructively evolve the model, avoid null values, and keep the information free from redundancies are gained. Performance issues due to extra joins are largely avoided thanks to a feature in modern database engines[when?] called join elimination or table elimination. In order to handle changes in the information content, anchor modeling emulates aspects of a temporal database in the resulting relational database schema.
History
In 2004 in Sweden came the earliest installations using anchor modeling were made when a data warehouse for an insurance company was built using the technique.
In 2007 the technique was being used in a few data warehouses and one online transaction processing (OLTP) system, and it was presented internationally by Lars Rönnbäck at the 2007 Transforming Data with Intelligence] (TDWI) conference in Amsterdam.[2] This stirred enough interest for the technique to warrant a more formal description. Since then research concerning anchor modeling is being done in a collaboration between the creators Olle Regardt and Lars Rönnbäck and a team at the Department of Computer and Systems Sciences, Stockholm University.
The first paper, in which anchor modeling is formalized, was presented in 2008 at the 28th International Conference on Conceptual Modeling and won the best paper award.[3]
A commercial web site provides material on anchor modeling which is free to use under a Creative Commons license. An online modeling tool is also available, which is free to use and is open source.[4]
Basic notions
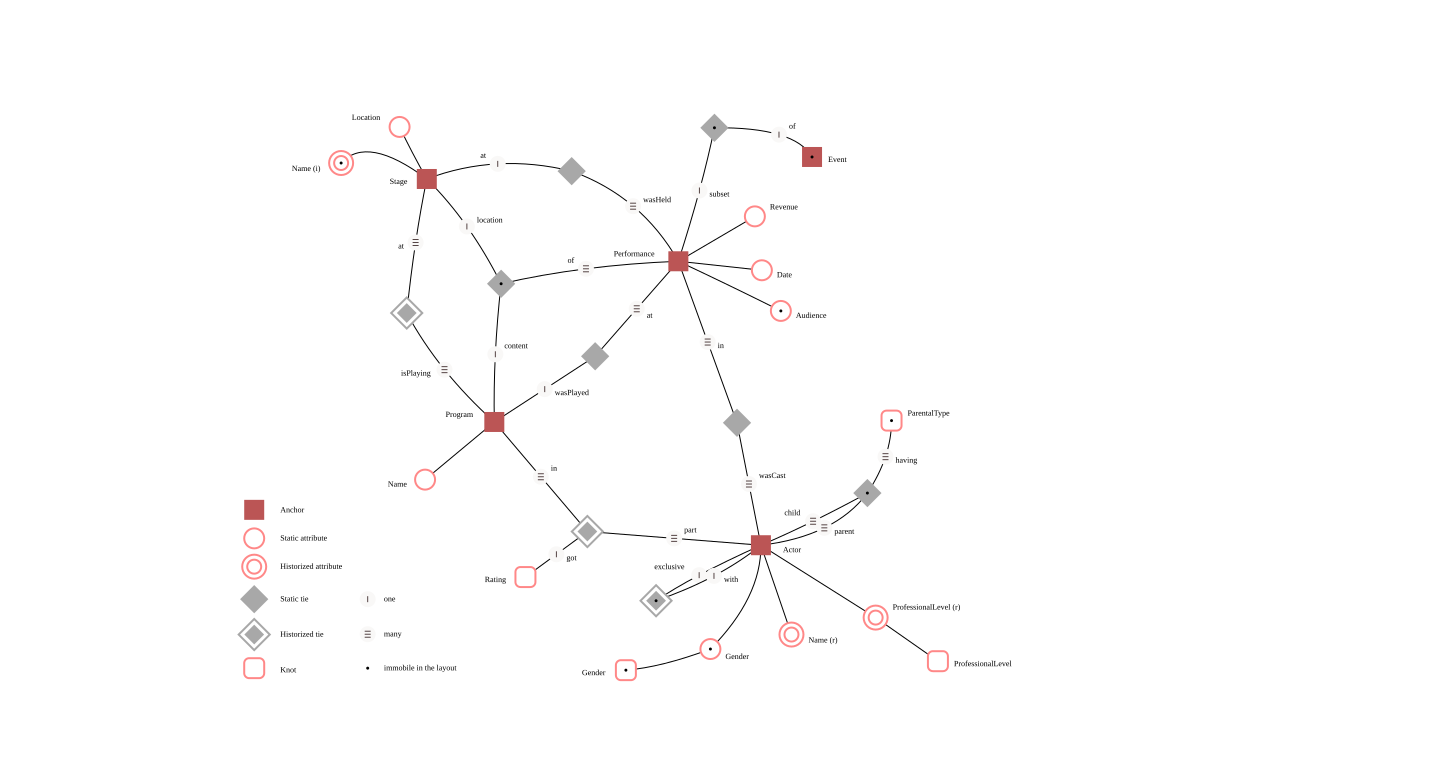
Anchor modeling has four basic modeling concepts: anchors, attributes, ties, and knots. Anchors are used to model entities and events, attributes are used to model properties of anchors, ties model the relationships between anchors, and knots are used to model shared properties, such as states. Attributes and ties can be historized when changes in the information they model need to be kept.
An example model showing the different graphical symbols for all the concepts can be seen below. The symbols resemble those used in entity–relationship modeling, with a couple of extensions. A double outline on an attribute or tie indicates that a history of changes is kept and the knot symbol (an outlined square with rounded edges) is also available.
Temporal aspects
Anchor modeling handles two types of informational evolution, structural changes and content changes. Changes to the structure of information is represented through extensions. The high degree of normalization makes it possible to non-destructively add the necessary modeling concepts needed to capture a change, in such a way that every previous schema always remains as a subset of the current schema. Since the existing schema is not touched, this gives the benefit of being able to evolve the database in a highly iterative manner and without causing any downtime.
Changes in the content of information is done by emulating similar features of a temporal database in a relational database. In anchor modeling, pieces of information can be tied to points in time or to intervals of time (both open and closed). The time points when events occur are modeled using attributes, e g the birth dates of persons or the time of a purchase. The intervals of time in which a value is valid are captured through the historization of attributes and ties, e g the changes of hair color of a person or the period of time during which a person was married. In a relational database this is achieved by adding a single column, with a data type granular enough to capture the speed of the changes, to the table corresponding to the historized attribute or tie. This adds a slight complexity as more than one row in the table have to be examined in order to know if an interval is closed or not.
Points or intervals of time not directly related to the domain being modeled, such as the points of time information entered the database, are handled through the use of metadata in anchor modeling, rather than any of the above-mentioned constructs. If information about such changes to the database needs to be kept bitemporal anchor modeling can be used, where in addition to updates, also delete statements become non-destructive.
Relational representation
In anchor modeling there is a one-to-one mapping between the symbols used in the conceptual model and tables in the relational database. Every anchor, attribute, tie, and knot have a corresponding table in the database with an unambiguously defined structure. A conceptual model can thereby be translated to a relational database schema using simple automated rules, and vice versa. This is different from many other modeling techniques in which there are complex and sometimes subjective translation steps between the conceptual, logical, and physical levels.
Anchor tables contain a single column in which identities are stored. An identity is assumed to be the only property of an entity that is always present and immutable. As identities are rarely available from the domain being modeled, they are instead technically generated, e g from an incrementing number sequence.
An example of an anchor for the identities of the nephews of Donald Duck is a set of 1-tuples:
{⟨#42⟩, ⟨#43⟩, ⟨#44⟩}
Knots can be thought of as the combination of an anchor and a single attribute. Knot tables contain two columns, one for an identity and one for a value. Due to storing identities and values together, knots cannot be historized. Their usefulness comes from being able to reduce storage requirements and improve performance, since tables referencing knots can store a short value rather than a long string.
An example of a knot for genders is a set of 2-tuples:
{⟨#1, 'Male'⟩, ⟨#2, 'Female'⟩}
Static attribute tables contain two columns, one for the identity of the entity to which the value belongs and one for the actual property value. Historized attribute tables have an extra column for storing the starting point of a time interval. In a knotted attribute table, the value column is an identity that references a knot table.
An example of a static attribute for their names is a set of 2-tuples:
{⟨#42, 'Huey'⟩, ⟨#43, 'Dewey'⟩, ⟨#44, 'Louie'⟩}
An example of a knotted static attribute for their genders is a set of 2-tuples:
{⟨#42, #1⟩, ⟨#43, #1⟩, ⟨#44, #1⟩}
An example of a historized attribute for the (changing) colors of their outfits is a set of 3-tuples:
{⟨#44, 'Orange', 1938-04-15⟩, ⟨#44, 'Green', 1939-04-28⟩, ⟨#44, 'Blue', 1940-12-13⟩}
Static tie tables relate two or more anchors to each other, and contain two or more columns for storing the identities. Historized tie tables have an extra column for storing the starting point of a time interval. Knotted tie tables have an additional column for each referenced knot.
An example of a static tie for the sibling relationship is a set of 2-tuples:
{⟨#42, #43⟩, ⟨#42, #44⟩, ⟨#43, #42⟩, ⟨#43, #44⟩, ⟨#44, #42⟩, ⟨#44, #43⟩}
The resulting tables will all be in sixth normal form except for ties in which not all columns are part of the primary key.
References
- ^ L. Rönnbäck; O. Regardt; M. Bergholtz; P. Johannesson; P. Wohed (2010). "Anchor modeling - Agile information modeling in evolving data environments". Data & Knowledge Engineering. 69 (12): 1229–1253. doi:10.1016/j.datak.2010.10.002. ISSN 0169-023X. (Preprint available here)
- ^ 6th TDWI European Conference - TDWI homepage Archived July 20, 2011, at the Wayback Machine
- ^ Regardt, Olle; Rönnbäck, Lars; Bergholtz, Maria; Johannesson, Paul; Wohed, Petia (2009). "Anchor Modeling". Proceedings of the 28th International Conference on Conceptual Modeling. ER '09. Gramado, Brazil: Springer-Verlag: 234–250. ISBN 978-3-642-04839-5.
- ^ Lars Rönnbäck. "Anchor Modeling Academy". Promotional website. Retrieved May 20, 2017.
