Debye–Hückel equation

The Debye-Hückel equation, named for its developers Peter Debye and Erich Hückel, provides one way to obtain activity coefficients ^[1]. Activities, rather than concentrations, are needed in many chemical calculations because solutions that contain ionic solutes do not behave as ideal solution even at very low concentrations. The activity is proportional to the concentration by a factor known as the activity coefficient $\gamma \,$, and takes into account the presence of other ions in the solution.

In order to calculate the activity of an ion in a solution, one must know the concentration and the activity coefficient, $\ \gamma \,$. The activity of some species C, $\ a_{C}\,$, is equal a dimensionless measure of concentration of C, $\ [C]\,$ multiplied by the activity coefficient of C, $\ \gamma \,$ for a given solution.

$\ a_{C}=\gamma {\frac {[C]}{[C_{\Theta }]}}\,$

Here :$\ [C_{\Theta }]\,$ represents the concentration of the chosen standard state, e.g. 1 mol/kg if we work in molality.

The Debye-Hückel Equation enables one to determine the activity coefficient of an ion in an aqueous solution of known ionic strength.

Debye-Hückel theory and the Debye length

The theory behind it was originally based on the idea that each ion is surrounded by an atmosphere-like cloud of ions of the opposite kind. A (inverse) measure for the radius of this cloud is known as the Debye length $\kappa \,$. Roughly speaking the radius = 1/κ.

The Debye length depends on the concentrations and carges of all ions or in other words the ionic strength I:

$\ \kappa ^{2}={\frac {1000N_{av}I}{\epsilon _{r}\epsilon _{0}k_{b}T}}\,$

$\ -ln(\gamma )={\frac {|q_{+}q_{-}|{\kappa }}{8\pi \epsilon _{r}\epsilon _{0}k_{b}T}}\,$

The activity coefficient obtained this way is actually the mean ionic activity γ_±

This law only holds in the limit that the concentration approaches zero and it known as the Debye-Hückel limiting law. In practice it only works at very small concentrations.

The Debye length is equally important for the stability of colloidal systems (DLVO theory) as it is for real solutions.

Extensions of the theory

A number of approaches have been proposed to extend the validity of the law to concentration ranges as commonly encountered in chemistry

The Extended Debye-Hückel Equation is given by:

$\ -log(\gamma )={\frac {Az^{2}{\sqrt {\mu }}}{1+Ba{\sqrt {\mu }}}}\,$

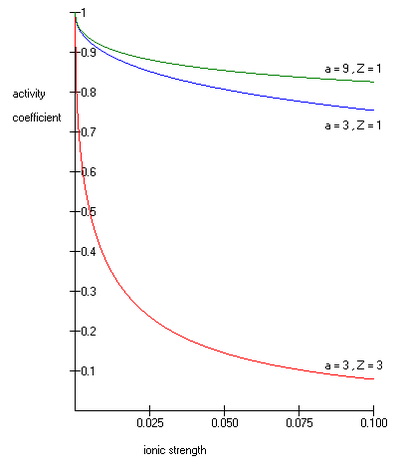
where $\ \gamma \,$ as its common logarithm is the activity coefficient, $\ z\,$ is the integer charge of the ion (1 for H^{+, 2 for Mg2+ etc.), $\ \mu \,$ is the ionic strength of the aqueous solution, and $\ a\,$ is the size or effective diameter of the ion in angstrom. The effective hydrated radius of the ion, a is the radius of the ion and its closely bound water molecules. Large ions and less highly charged ions bind water less tightly and have smaller hydrated radii than smaller, more highly charged ions. Typical values are 3Å for ions such as H+,Cl-,CN-, and HCOO-. The effective diameter for the hydronium ion is 9Å. $\ A\,$ and $\ B\,$ are constants with values of respectively 0.5085 and 0.3281 at 25°C in water [2].}

The Extended Debye-Hückel Equation provides accurate results for μ ≤ 0.1 M. For solutions of greater ionic strengths, the Pitzer equation should be used. In these solutions the activity coefficient may actually increase with ionic strength.

The Debye-Hückel plot with different values for ion charge Z and ion diameter a

The Debye-Hückel Equation cannot be used in the solutions of surfactants where the presence of micelles influences on the electrochemical properties of the system (even rough judgement overestimates γ for ~50%).

External links

• For easy calculation of activity coefficients in (non-micellar) solutions, check out the IUPAC open project Aq-solutions (freeware).
• Gold Book definition

References

1. ^ Quantitative Chemical Analysis, 6th Edition; Harris, Daniel C.; W. H. Freeman & Company, 2003. ISBN 0-7167-4464-3
2. ^ Fundamentals of Analytical Chemistry, Douglas A. Skoog, ISBN 0534417965