Jump to content

Ray tracing (graphics)

From Wikipedia, the free encyclopedia

This is an old revision of this page, as edited by 70.233.144.255 (talk) at 22:11, 24 February 2007 (→In optical design). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

A ray-traced scene

Ray tracing is a general technique from geometrical optics of modeling the path taken by light by following rays of light as they interact with optical surfaces. It is used in the design of optical systems, such as camera lenses, microscopes, telescopes and binoculars. The term is also applied to mean a specific rendering algorithmic approach in 3D computer graphics, where mathematically-modelled visualisations of programmed scenes are produced using a technique which follows rays from the eyepoint outward, rather than originating at the light sources. It produces results similar to ray casting and scanline rendering, but facilitates more advanced optical effects, such as accurate simulations of reflection and refraction, and is still efficient enough to frequently be of practical use when such high quality output is sought.

Broad description of ray tracing computer algorithm

Three spheres that reflect off the floor and each other

Ray tracing describes a method for producing visual images constructed in 3D computer graphics environments, with more realism than either ray casting or scanline rendering techniques. It works by tracing, in reverse, a path that could have been taken by a ray of light which would intersect the imaginary camera lens. As the scene is traversed by following in reverse the path of such rays, visual information on the appearance of the scene is built up as viewed from the point of view of the camera. The ray's reflection, refraction, or absorption are calculated when it intersects objects and media in the scene.

Scenes in raytracing are described mathematically, usually by a programmer, or by a visual artist using intermediary tools. Scenes may also incorporate data from images and models captured by various technological means, for instance digital photography.

Following rays in reverse is many orders of magnitude more efficient at building up the visual information than would be a genuine simulation of all possible light interactions in the scene, since the overwhelming majority of light rays from a given light source do not wind up providing significant light to the viewer's eye. (Instead they may bounce around until they diminish to almost nothing, or bounce off to infinity, or perhaps intersect some other viewer's eye.) A computer simulation which started with the rays emitted by each light source and searched for the ones which would wind up intersecting the desired viewpoint would not be practically feasible.

The shortcut taken in raytracing, then, is to pre-suppose that a given ray ends up at the viewpoint, then trace backwards. After a stipulated number of maximum reflections has occurred, the light intensity of the point of last intersection is computed using a number of algorithms, which may include the classic rendering algorithm, and may perhaps incorporate other techniques such as radiosity.

Detailed description of ray tracing computer algorithm and its genesis

What happens in nature

In nature, a light source emits a ray of light which travels, eventually, to a surface that interrupts its progress. One can think of this "ray" as a stream of photons traveling along the same path. In a perfect vacuum this ray will be a straight line. In reality, any combination of three things might happen with this light ray: absorption, reflection, and refraction. A surface may reflect all or part of the light ray, in one or more directions. It might also absorb part of the light ray, resulting in a loss of intensity of the reflected and/or refracted light. If the surface has any transparent or translucent properties, it refracts a portion of the light beam into itself in a different direction while absorbing some (or all) of the spectrum (and possibly altering the color). Between absorption, reflection, and refraction, all of the incoming light must be accounted for, and no more. A surface cannot, for instance, reflect 66% of an incoming light ray, and refract 50%, since the two would add up to be 116%. From here, the reflected and/or refracted rays may strike other surfaces, where their absorptive, refractive, and reflective properties are again calculated based on the incoming rays. Some of these rays travel in such a way that they hit our eye, causing us to see the scene and so contribute to the final rendered image.

Ray casting algorithm

The first ray casting (versus ray tracing) algorithm used for rendering was presented by Arthur Appel in 1968. The idea behind ray casting is to shoot rays from the eye, one per pixel, and find the closest object blocking the path of that ray - think of an image as a screen-door, with each square in the screen being a pixel. This is then the object the eye normally sees through that pixel. Using the material properties and the effect of the lights in the scene, this algorithm can determine the shading of this object. The simplifying assumption is made that if a surface faces a light, the light will reach that surface and not be blocked or in shadow. The shading of the surface is computed using traditional 3D computer graphics shading models. One important advantage ray casting offered over older scanline algorithms is its ability to easily deal with non-planar surfaces and solids, such as cones and spheres. If a mathematical surface can be intersected by a ray, it can be rendered using ray casting. Elaborate objects can be created by using solid modeling techniques and easily rendered.

Ray casting for producing computer graphics was first used by scientists at Mathematical Applications Group, Inc., (MAGI) of Elmsford, New York, New York. In 1966, the company was created to perform radiation exposure calculations for the Department of Defense. MAGI's software calculated not only how the gamma rays bounced off of surfaces (ray casting for radiation had been done since the 1940s), but also how they penetrated and refracted within. These studies helped the government to determine certain military applications ; constructing military vehicles that would protect troops from radiation, designing re-entry vehicles for space exploration. Under the direction of Dr. Philip Mittelman, the scientists developed a method of generating images using the same basic software. In 1972, MAGI became a commercial animation studio. This studio used ray casting to generate 3-D computer animation for television commercials, educational films, and eventually feature films – they created much of the animation in the film Tron using ray casting exclusively. MAGI went out of business in 1985.

Ray tracing algorithm

The next important research breakthrough came from Turner Whitted in 1979. Previous algorithms cast rays from the eye into the scene, but the rays were traced no further. Whitted continued the process. When a ray hits a surface, it could generate up to three new types of rays: reflection, refraction, and shadow. A reflected ray continues on in the mirror-reflection direction from a shiny surface. It is then intersected with objects in the scene; the closest object it intersects is what will be seen in the reflection. Refraction rays traveling through transparent material work similarly, with the addition that a refractive ray could be entering or exiting a material. To further avoid tracing all rays in a scene, a shadow ray is used to test if a surface is visible to a light. A ray hits a surface at some point. If the surface at this point faces a light, a ray (to the computer, a line segment) is traced between this intersection point and the light. If any opaque object is found in between the surface and the light, the surface is in shadow and so the light does not contribute to its shade. This new layer of ray calculation added more realism to ray traced images.

Advantages of ray tracing

Ray tracing's popularity stems from its basis in a realistic simulation of lighting over other rendering methods (such as scanline rendering or ray casting). Effects such as reflections and shadows, which are difficult to simulate using other algorithms, are a natural result of the ray tracing algorithm. Relatively simple to implement yet yielding impressive visual results, ray tracing often represents a first foray into graphics programming.

Disadvantages of ray tracing

A serious disadvantage of ray tracing is performance. Scanline algorithms and other algorithms use data coherence to share computations between pixels, while ray tracing normally starts the process anew, treating each eye ray separately. However, this separation offers other advantages, such as the ability to shoot more rays as needed to perform anti-aliasing and improve image quality where needed. Although it does handle interreflection and optical effects such as refraction accurately, traditional Ray Tracing is also not necessarily photorealistic. True photorealism occurs when the rendering equation is closely approximated or fully implemented. Implementing the rendering equation gives true photorealism, as the equation describes every physical effect of light flow. However, this is usually infeasible given the computing resources required. The realism of all rendering methods, then, must be evaluated as an approximation to the equation, and in the case of Ray Tracing, it is not necessarily the most realistic. Other methods, including photon mapping, are based upon ray tracing for certain parts of the algorithm, yet give far better results.

Reversed direction of traversal of scene by the rays

The process of shooting rays from the eye to the light source to render an image is sometimes referred to as backwards ray tracing, since it is the opposite direction photons actually travel. However, there is confusion with this terminology. Early ray tracing was always done from the eye, and early researchers such as James Arvo used the term backwards ray tracing to refer to shooting rays from the lights and gathering the results. As such, it is clearer to distinguish eye-based versus light-based ray tracing. Research over the past decades has explored combinations of computations done using both of these directions, as well as schemes to generate more or fewer rays in different directions from an intersected surface. For example, radiosity algorithms typically work by computing how photons emitted from lights affect surfaces and storing these results. This data can then be used by a standard recursive ray tracer to create a more realistic and physically correct image of a scene. In the context of global illumination algorithms, such as photon mapping and Metropolis light transport, ray tracing is simply one of the tools used to compute light transfer between surfaces.

Algorithm: classical recursive ray tracing

For each pixel in image {
  Create ray from eyepoint passing through this pixel
  Initialize NearestT to INFINITY and NearestObject to NULL

  For every object in scene {
     If ray intersects this object {
        If t of intersection is less than NearestT {
           Set NearestT to t of the intersection
           Set NearestObject to this object
        }
     }
  }

  If NearestObject is NULL {
     Fill this pixel with background color
  } Else {
     Shoot a ray to each light source to check if in shadow
     If surface is reflective, generate reflection ray: recurse
     If surface is transparent, generate refraction ray: recurse
     Use NearestObject and NearestT to compute shading function
     Fill this pixel with color result of shading function
  }
}

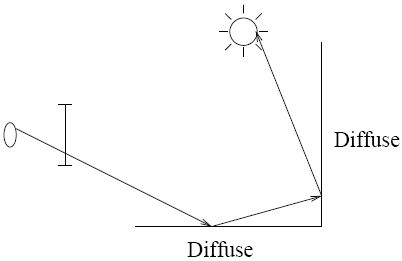
Below is an image showing a simple example of a path of rays recursively generated from the camera (or eye) to the light source using the above algorithm. A diffuse surface reflects light in all directions.

First, a ray is created at an eyepoint and traced through a pixel and into the scene, where it hits a diffuse surface. From that surface the algorithm recursively generates a reflection ray, which is traced through the scene, where it hits another diffuse surface. Finally, another reflection ray is generated and traced through the scene, where it hits the light source and is absorbed. The color of the pixel now depends on the colors of the first and second diffuse surface and the color of the light emitted from the light source. For example if the light source emitted white light and the two diffuse surfaces were blue, then the resulting color of the pixel is blue.

Ray tracing in real time

There has been some effort for implementing ray tracing in real time speeds for interactive 3D graphics applications such as demoscene productions, computer and video games.

The OpenRT project includes a highly-optimized software core for ray tracing along with an OpenGL-like API in order to offer an alternative to the current rasterization based approach for interactive 3D graphics.

Ray tracing hardware, such as the experimental Ray Processing Unit developed at the Saarland University, has been designed to accelerate some of the computationally intensive operations of ray tracing.

Some real-time software 3D engines based on ray tracing have been developed by hobbyist demo programmers since the late 1990s. The ray tracers used in demos, however, often use inaccurate approximations and even cheating in order to attain reasonably high frame rates. [1]

In optical design

Ray tracing in computer graphics derives its name and principles from a much older technique used for lens design since the 1900s. Geometric ray tracing is used to describe the propagation of light rays through a lens system or optical instrument, allowing the image-forming properties of the system to be modeled. The following effects can be integrated into a ray tracer in a straight forward fashion, but are omitted in computer graphics leading to an unnecessary branching (software):

For the application of lens design two special cases of interference is important. In a focus rays from a point light source meet again. In a closeup of the focal region all rays are replaced by plane waves. They inherit their direction from the rays. The optical path length from the light source is used for the phase. The derivative of the position of the ray in the focal region on the source position is used to get the width of the ray and from that the amplitude of the plane wave. The result is the point spread function, its Fourier transform is the MTF, and from the former the Strehl ratio can be calculated also. The other case is wavefront calculation of a plane wavefront. Of course when the rays come to close together or even cross the wavefront approximation breaks down. Interference of spherical waves is usually not combined with ray tracing thus diffraction at an aperture cannot be calculated.

This is used to optimize the design of the instrument by minimizing aberrations, for photography, and for longer wavelength applications such as designing microwave or even radio systems, and for shorter wavelengths, such as ultraviolet and X-ray optics.

Before the advent of the computer, ray tracing calculations were performed by hand using trigonometry and logarithmic tables. The optical formulas of many classic photographic lenses were optimized by rooms full of people, each of whom handled a small part of the large calculation. Now they are worked out in optical design software such as OSLO or TracePro from Lambda Research, Code-V or Zemax. A simple version of ray tracing known as ray transfer matrix analysis is often used in the design of optical resonators used in lasers.

Example

As a demonstration of the principles involved in raytracing, let us consider how one would find the intersection between a ray and a sphere. The general equation of a sphere can be expressed in Vector notation, where I is a point on the surface of the sphere, C is its center and r is its radius, is . Equally, if a line is defined by its starting point S (consider this the starting point of the ray) and its direction d (consider this the direction of that particular ray), each point on the line may be described by the expression

where t is a constant defining the distance along the line from the starting point (hence, for simplicity's sake, d is generally a unit vector). Now, in the scene we know S, d, C, and r. Hence we need to find t as we substitute in for I:

Let for simplicity, then

Now this quadratic equation has solution(s):

If the quantity under the square-root is negative, then the ray does not intersect the sphere. This is merely the math behind a straight ray-sphere intersection. There is of course far more to the general process of raytracing, but this demonstrates an example of the algorithms used.

See also

Software

References

  • Glassner, Andrew (Ed.) (1989). An Introduction to Ray Tracing. Academic Press. ISBN 0-12-286160-4.
  • Shirley, Peter and Morley Keith, R. (2001) Realistic Ray Tracing,2nd edition. A.K. Peters. ISBN 1-56881-198-5.
  • Henrik Wann Jensen. (2001) Realistic image synthesis using photon mapping. A.K. Peters. ISBN 1-56881-147-0.
  • Pharr, Matt and Humphreys, Greg (2004). Physically Based Rendering : From Theory to Implementation. Morgan Kaufmann. ISBN 0-12-553180-X.

Raytracing software

Template:Link FA

Retrieved from "https://en.wikipedia.org/w/index.php?title=Ray_tracing_(graphics)&oldid=110676141"