User:Fropuff/Drafts/Hom functor

Representable functor

Definition

Let C be an locally small category and let Set be the category of sets. For each object A in C let Hom(A,–) be the hom-functor which maps objects X to the set Hom(A,X). A functor F : C → Set is said to be representable if it is naturally isomorphic to Hom(A,–) for some object A in C. A representation of F is a pair (A, Φ) where

Φ : Hom(A,–) → F

is a natural isomorphism.

A dual set of definitions and statements apply to contravariant functors. A contravariant functor G : C → Set is said to representable if it is naturally isomorphic to the hom-functor Hom(–,A) for some object A in C.

Yoneda's lemma and universal elements

Recall that a natural isomorphism Φ from Hom(A,–) to F is determined by a family of bijections bijections Φ_X : Hom(A,X) → F(X) making a certain set of diagrams commute. Define

$\varphi =\Phi _{A}(\mathrm {id} _{A})\in F(A).$

The natural isomorphism is completely determined by φ since for each morphism u : A → X one has

$\Phi _{X}(u)=(Fu)(\varphi ).$

One says that the functor F is represented by the pair (A, φ).

The representing pair (A,φ) is unique in the following sense. If (A₁,φ₁) and (A₂,φ₂) represent the same functor, then there exists one and only one isomorphism from A₁ to A₂ so that φ₁ in F(A₁) maps to φ₂ in F(A₂). This is because we have the isomorphisms Φ₁:Hom_C(A₁,-)→F and Φ₂:Hom_C(A₂,-)→F and so we have an isomorphism (Φ₂)^-1 o Φ₁:Hom_C(A₁,-)→Hom_C(A₂,-). By the Yoneda lemma, A₁ is isomorphic to A₂ via the isomorphism determined by Φ₁ and Φ₂, and this maps φ₁ to φ₂. Uniqueness follows as everything is determined by φ₁ and φ₂.

Yoneda's lemma

Formal statement

Let C be a locally small category (i.e. the hom-sets of C are actual sets and not proper classes). For each object A of C let

$h_{A}=\mathrm {Hom} (A,-)\colon {\mathcal {C}}\to \mathbf {Set}$

be the hom-functor that sends X to the hom-set Hom(A,X).

Let F be an arbitrary functor from C to Set. Yoneda's lemma says that for each object A of C the natural transformations from h_A to F are in one-to-one correspondence with the elements of F(A):

$\mathrm {Nat} (h_{A},F)\cong F(A).$

Given a natural transformation Φ from h_A to F, the corresponding element of F(A) is

$u=\Phi _{A}(\mathrm {id} _{A})\in F(A).$

The proof of Yoneda's lemma is indicated by the the following commutative diagram:

Proof of Yoneda's lemma

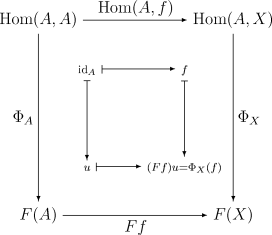
This diagram shows that the natural transformation Φ is completely determined by u since for each morphism f : A → X one has

$\Phi _{X}(f)=(Ff)u.\,$

Moreover, any element u ∈ F(A) defines a natural transformation in this way.

The is a dual version of Yoneda's lemma that applies to contravariant functors from C to Set. Here one lets

$h_{A}=\mathrm {Hom} (-,A)\,$

be the contravariant hom-functor. The statement and proof are as above.

Limit (category theory)

Let F : J → C be a functor with J small, and let Δ : C → C^J be the diagonal functor (i.e. Δ(X) : J → C is the constant functor to X). Then following statements are equivalent:

• (N, ψ) is a cone to F
• ψ is a natural transformation from Δ(N) to F
• (N, ψ) is a object in the comma category (Δ ↓ F)

The limit of F, a universal cone (L, φ) to F, is then nothing but a universal morphism from Δ to F, or a terminal object in (Δ ↓ F)

The dual statements are also equivalent:

• (N, ψ) is a cone from F
• ψ is a natural transformation from F to Δ(N)
• (N, ψ) is a object in the comma category (F ↓ Δ)

The colimit of F, a universal cone (L, φ) from F, is then nothing but a universal morphism from F to Δ, or an initial object in (F ↓ Δ)

Comma categories

comma category (T ↓ S)

File:CommaCategory-03.png

• hom-set category (A ↓ B) = Hom(A, B) as a discrete category
• morphism (or arrow) category (C ↓ C) = C²
• (U ↓ A), objects U over A, or morphisms from U to A
  • slice category, objects over A, written (C ↓ A) or C/A
  • (Δ ↓ F) category of cones to F
• (A ↓ U), objects U under A, or morphisms from A to U
  • coslice category, objects under A, written (A ↓ C) or A/C
  • (F ↓ Δ) category of cones from F

Slice category

Let C be a category and let A be an object in C. The slice category is denoted (C ↓ A) or C/A.

• objects are morphisms to A in C, e.g. f : X → A
• morphisms are commutative triangles φ : (f : X → A) → (g : Y → A) with f = gφ

The forgetful functor, U : C/A → C, assigns to each morphism f : X → A its domain X. If C has finite products this functor has a right-adjoint which assigns to each space Y the projection map (A × Y → A). U then commutes with colimits.

Colimits

• If I is an initial object in C then (I → A) is an initial object in C/A.
• The coproduct of f_X and f_Y is the natural morphism f_X+Y.

Limits

• (id_A : A → A) is a terminal object in C/A.
• Products in C/A are pullbacks in C.

Examples

• If A is terminal, then C/A is isomorphic to C.
• If C is a poset category, C/A is the principal ideal of objects less than A.
• Set/ℕ is the category of graded sets (morphisms must preserve the grade, so perhaps different than a multiset)