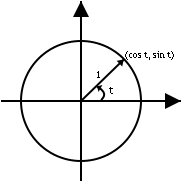
Unit circle

Illustration of a unit circle.
t is an angle measure.
Larger image with several angles labeled

In mathematics, a unit circle is a circle with unit radius, i.e., a circle whose radius is 1. Frequently, especially in trigonometry, "the" unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Euclidean plane. The unit circle is often denoted by S¹.

The variables x and y for every point (x, y) on the unit circle in the first quadrant are the lengths of the legs of a right triangle with hypotenuse length 1. Therefore, the Pythagorean theorem states that x and y are related by:

$x^{2}+y^{2}=1\,\!$

Since x² = (-x)² for all x, the above equation is valid for points where x or y are negative as well (i.e. not in the first quadrant).

One may also use other notions of "distance" to define other "unit circles"; see the article on normed vector space for examples.

Trigonometric functions in the unit circle

In a unit circle, several interesting things relating to trigonometric functions may be defined, with the given notation:

A point on the unit circle, pointed to by a certain vector from the origin with the angle t from the x-axis, has the coordinates:

$x=\cos(t)\,\!$

$y=\sin(t)\,\!$

The equation of the circle above also immediately gives us the well-known "trigonometric 1":

$\cos ^{2}(t)+\sin ^{2}(t)=1\,\!$

The unit circle also gives an intuitive way of realizing that sine and cosine are periodic functions, with the identities

$\cos(t)=\cos(2\pi k+t)\,\!$

$\sin(t)=\sin(2\pi k+t)\,\!$

for any integer k.

These identities come from the fact that (x,y) coordinates remain the same after the angle t is increased or decreased by one revolution in the circle (2π). The notion of sine, cosine, and other trigonometric functions only makes sense with angles more than zero or less than π/2 when working with right triangles, but in the unit circle, angles outside this range have sensible, intuitive meanings.

As a group

The multiplication of two complex numbers makes the unit circle into a group, called the circle group, when the point

$(\cos \theta ,\sin \theta )\,\!$

is identified with

$e^{i\theta }\,\!$

The group law is to take the sum of the angles, modulo integer multiples of 2π. The circle group is also called U(1), the first unitary group, which points out its basic place in the theory of Lie groups. In fact the circle group is a compact Lie group, and any compact Lie group G of dimension ≥ 1 has a subgroup isomorphic with it. That means that, thinking in terms of symmetry, a compact symmetry group acting continuously can be expected to have one-parameter circle subgroups acting; the consequences in physical systems are seen for example at rotational invariance, and spontaneous symmetry breaking.

The circle group has many subgroups, but its only closed subgroups consist of roots of unity: there is one such, that is cyclic of order n, for each integer n ≥ 1.

See also

• Trigonometric function
• Angle measure
• Unit square