User talk:Huon
- /Archive1 December 2005 to August 2006
RebDrummer61 13:40, 4 September 2006 (UTC)
I thank you for the editing you did on my (and now also yours to a certain degree) Albert Ellmenreich article. I could only roughly translate some of his works. Thanks again. Update: My same graditude for The Spinning Song article.
Küsnacht -> Hombrechtikon
Thanks for picking up the slip-up I made here. I'll go back and check I didn't make any similar ones. --BillC 17:18, 7 September 2006 (UTC)
Yechezkel Levenstein
I responded on my talk page. Jon513 18:17, 13 September 2006 (UTC)
Locality, Non-locality and the Real-line
Hi Houn,
Definition 1 is: A and (x xor y)
A is a non-local urelement, where x or y are local urelements.
Something that I wrote in my personal forum:
Z is a place holder of the Context concept.
A, B, C, ... are place holders of independent and self-consistent mathematical objects (axioms).
Z without A, B, C, ... is not an interesting mathematical framework.
If Z does not exist, than A, B, C, ... have nothing in common, and no axiomatic system of more than a single axiom can be found (logically, all we have is A xor B xor C xor ...)
For example:
A___B___C___...
1 xor 0 xor 0 xor ... --> true
0 xor 1 xor 0 xor ... --> true
0 xor 0 xor 1 xor ... --> true
...
So, without at least Z and (A xor B) complementation, no interesting mathematical framework can be found.
Again,
This work was presented as a "short communication" under the name "Complementary Mathematics" (the presentation can be seen in http://www.createforum.com/phpbb/viewtopic.php?t=60&mforum=geproject ) by my colleague Moshe Klein in http://icm2006.org/v_f/web_fr.php at 25.8 17:15 at room 403r and after the presentation, more than 40 mathematicians wished to get a copy of the work. Also I personally presented it to Benoit Mandelbrot and he was exited by the new mathematical possibilities of this work. DoronSahdmi 22:02, 14 September 2006 (UTC)
- Now I understand less than before. If definition 1 requires the reader to know what local and non-local Ur-elements are, even though locality and non-locality are given later in definitions 6 and 7, respectively, isn't that circular reasoning? Or is definition 1 supposed to be understood only later, after other, preliminary definitions have been made?
- I'm sorry to say so, but the entire introduction looks like pseudo-mathematical gibberish. I assume some new concept of "membership" shall be introduced, and definition 1 shall be the "logical basis" for it, but it does not mention membership at all!
- Furthermore, the concept of non-locality does not only introduce a new kind of set theory, but a new kind of logic. If a non-local element exists, then both a statement (x€A) and its negation can be true at the same time. This is rather unhelpful. For example, even if your new framework allows you to prove that 0.9999...<1, the negation of this statement, 0.9999...>=1, could still be true as well, couldn't it? Once you disregard the law of noncontradiction, you are hard-pressed to show that any statement isn't true (just showing the converse is true doesn't help).
- You might try to salvage your approach along the following lines:
- Let a class of objects be given. Then membership and non-membership are two relations between objects satisfying the following axioms:
- Let x and y be objects. x is a member of y or x is a non-member of y (or both).
- If an object A is a set and an object x is an element of A, then it is also a member of A.
- Definition: An object x is called local if for all objects A, x is not both a member of A and a non-member of A. Otherwise, it is called non-local.
- Let a class of objects be given. Then membership and non-membership are two relations between objects satisfying the following axioms:
- Now you might add further axioms, but these should be some basics. Note that being a non-member here is not the negation of being a member. By axiom 1, not being a member implies being a non-member, but the converse may be false. This approach allows me to still follow usual logic; I might even apply Zermelo-Fraenkel set theory (unless it really is important that some of my elements are not sets themselves).
- Concerning the ICM talk, I admit I'm impressed, but agree with Melchoir: Get it published, and then let's see. --Huon 09:39, 15 September 2006 (UTC)
Hi Houn,
You steel look at my system from the standard point of view, which is based only on local objects and a membership between local only objects.
So, here is again the logical basis of a local object and a non-local object.
The standard Set/Member relation is based on a xor connective.
For example: Any given x is (a member) xor (not a member) of set A and there is no intermediate state.
Fuzzy logic expands standard membership (0 xor 1) by using x, which defines the degree of a membership between 0 and 1 (0 or 1 are included too).
If 0<x<1, and [0,x] belongs to set A then (x,1] does not belong to set A ( [0,x] xor (x,1] ) So, in both cases a xor connective is used as the logical basis of the Set/Member relations.
0, 1, [0,x] or (x,1] (where 0<x<1) are all local mathematical objects because we can clearly define their locality (they are "in" xor "out" of some mathematical object).
An object that is not a set but can be a member of a set, is called an urelemnt ( http://72.14.221.104/search?q=cache:JRO16vlJWNQJ:en.wikipedia.org/wiki/Urelement+urelement&hl=en&ct=clnk&cd=1 ).
A sub-object is a part of an object.
Since an urelement is not a set, it does include any sub-object as a part of it, or in other words, it is an atomic singleton.
x is a urelement.
If x is a member and not a member of A then x is a non-local mathematical object.
The best way to notate this is: _{_} , where __ is a urelement.
__ can be both a local ( {__} xor __{ } ) or a non-local ( _{_} ) urelement.
In the case of ( {__} xor __{ } ) __ is not a non-local urelement singletone, but it is a one_of_many element that is based on (x € A xor x not_€ A --> local object).
Non-locality exist only if __ is not a one_of_many object (a singleton) that is based on (x € A and x not_€ A --> non-local object).
If we wish to find the best way to notate a local urelement (a local atomic singleton) than we use . (a point).
An example: {.} xor .{ }
In the standard Set/Member relations each member is a sub-object xor not a sub-object of a set, and both the empty and any a non-empty set are defined by the ways that these sub-objects belong xor don't belong to them.
Since . and __ are atomic singletons, they are not defined by each other (they are mutually independent exactly like two axioms) and we can expand the membership concept beyond the Set/Member dependency.
n>1
k=n-1
If we are using a membership among mutually independent objects, then 0.kkk...[base n] < 1
If the Real-line is a non-local urelement, than 0.kkk… is not the real number 1 but it is the non-local number 0.kkk…[base n] which is smaller than the real number 1.
Here is a part of my work, which is related to this subject:
5. Locality, non-locality and the real-line
A sequence is a collection of elements ordered by some rule. A continuum is a property of a non-local urelement. If we define the real line as a non-local urelement, then no sequence is a continuum. By studying locality and non locality along the real line, we discovered a new type of numbers, the non-local numbers. For example,
Figure 5
Figure 5 illustrates a proof that the number 0.111… is not a representation of the number 1 in base 2, but the non-local number 0.111… < 1. Are there any numbers between 0.111… and 1? Yes, for any given base n>2, the non-local number 0.kkk… where k=n-1. For example:
Figure 6
Figure 6 demonstrates that between any given pair of R members, which are local numbers, there exists a non-local number, whose exact location on the real line does not exist. A local number is not a limit of any non-local number, because local and non-local numbers are mutually independent. Furthermore, no set of infinitely many elements can reach the completeness of a non-local urelement. Thus, any non-finite set is an incomplete mathematical object, when compared to a non-local urelement.
As for your questions:
You write:
- For example, even if your new framework allows you to prove that 0.9999...<1, the negation of this statement, 0.9999...>=1, could still be true as well, couldn't it?
An Answer:
- In my system 0____1 is a non-local urelement (x€A and x not_€ A) where 0.999... is not a limit of a sequence (as it understood by the standard system) but a non-local number, which is a non-finite object upon non-finite scales of [base n] levels.
- 0.kkk... [base n] is not an R member, therefore no R member is its limit.
- As a result, 0.kkk... [base n] < 0____1 .
You write:
- Once you disregard the law of noncontradiction, you are hard-pressed to show that any statement isn't true (just showing the converse is true doesn't help).
My answer:
- In my system, the law of contradiction is a the particular case of x xor y if you ignore A as a common context of x,y .
- If you do not ignore A then you have at least A and (x xor y).
- A is a non-local urelement, and x,y are local elements.
- My system deals with the COMPLEMENTARY relations that exist between the non-local (A) and the local (x,y), where the non-local number 0.kkk... is a product of these relations (in the standard framework, which is based on the law of contradiction between local-only objects, the non-local number 0.kkk... does not exist) and not a representation of the real number 1 (each R member is a local-only mathematical object that is based on x € A xor x not_€ A --> . )
- This kind of a mathematical reseach is beyond any framework which is based only on the local (as the standard framework does).
- Again, A is a non-local object (which is not less than ___), x,y,... are local ojcets (where each one of them is no more than . ).
- In the level of x xor y __ does not exist, and in the level of ___ x xor y do not exist.
- My system is based on the reseach of the memberships' products between
- (x € A and x not_€ A --> __) and (x € A xor x not_€ A --> .)
- Again, my system researches the mathematical universe that exists between a non-local urelement, which is not a one_of_many object (it is x € A and x not_€ A --> __ singleton), and a set of local objects (where each local object is a one_of_meny
- x € A xor x not_€ A --> . object).
- Since each existing product of this universe is the result of the relations between "father" non-locality and "mother" locality, then complementarity not--> contradiction.
- First of all, you seem to have misunderstood fuzzy logic. That's not about intervals being inside or outside some set ("[0,x] belongs to set A", as you write); instead, whether or not an element e is contained in some set A is not given by the binary values "yes" or "no", but by a real number between 0 and 1 (where 1 corresponds to "e is an element of A" and 0 to "e is not an element of A"). But since e can also just be "somewhat of an element of A" (at the same time being "somewhat not an element of A", too), that's hardly based on xor.
- Next, let's consider the sentence: "Since an urelement is not a set, it does include any sub-object as a part of it, or in other words, it is an atomic singleton." I agree that an urelement is not a set (by definition), but why then should it have "parts"? What is a "part" of an element? I don't know what an "atomic singleton" is, and a Google search seemed to indicate some sort of programming term; I'll just take this sentence as a definition.
- On second thought, it occured to me that you might just mean that there are no elements of an urelement, since an urelement is not a set. Is that what you meant?
- Next, "if x is a member and not a member of A", then you have at least one statement ("x is a member of A") which is both true and false at the same time. Obviously your new brand of logic has to allow such statements. I still don't understand if and why only some statements should be allowed this ambiguity. Why shouldn't the statement "0.999... is an element (or, if you prefer, a member) of the set of numbers less than 1" also be both true and false at the same time? I read your answer, but could not understand it. What is a "non-finite object upon non-finite scales of [base n] levels" supposed to be? What are the "levels" you speak of? And if, as you write, "0.kkk... [base n] is not an R member", how can you compare it to either 1 or 0___1? The relation "less than" is usually only defined on numbers, especially on real numbers.
- Then you write "the law of contradiction is a the particular case of x xor y if you ignore A as a common context of x,y". That's a good example of what I called pseudo-mathematical gibberish. I wasn hardly able to follow your grammar here, much less the mathematics. And "If you do not ignore A then you have at least A and (x xor y)" doesn't help. A is a non-local urelement such as a line, correct? And x,y are two local urelements such as points, right? Then what's Point1 xor Point2 supposed to be? x, y and A would have to be statements, either true or false, in order to connect them via xor and and. Anyway, the law of contradiction hardly is just a special case of "x xor y". The law doesn't only say "P xor not-P", it says this statement is true (while in general, x xor y may be true or false).
- The next definition I can't follow is this: "If we define the real line as a non-local urelement..." Is any non-local urelement the real line? That's what you say, but I doubt it's what you mean. The inference you draw, that no sequence is a continuum, is one I can agree with, both in standard mathematics and in your version (why should "a collection of elements ordered by some rule" be "a property of a non-local urelement"? Why shoud this even depend on what we define the real line to be?).
- In general, I'm surprised about your use of the "real line". You surely know that in standard mathematics, the real numbers are the result of a long-winded construction, starting with the natural numbers and evolving through the integers and the rationals. In effect, real numbers usually are equivalence classes of Cauchy sequences of elements of the quotient field of the Grothendieck group (which happens to be a ring) of the natural numbers. Does this construction still work in your framework? Shouldn't you instead construct "organic reals" out of organic natural numbers? If so, how precisely? Are the "organic reals" ordered? Are even the organic natural numbers ordered?
- I think this has grown long enough for now... Yours, Huon 20:05, 15 September 2006 (UTC)
You write:
- First of all, you seem to have misunderstood fuzzy logic.
My answer:
- It depends of how you understand x as a partial membership between 0 and 1.
- As I understand it, by using x, where x is 0 < x < 1, then x is not a single member of A, but the value that precisely determinates how much of [0,1](= R set) is a member of A (or in other words ( [0,x] is a member of A xor (x,1] is not a member of A).
- If x is a gray level between totally white (0) and totally black (1), than gray is not a basic color but the result of a mixing between 0,1 totalities. In this case there is a xor connective between x and its complement to 1 (for example: x is 20%"in" xor 80%"out" A).
- If [0________1] is R set (and in this case ____ is not a non-local urelement, but it is a totally ordered set of points-like objects) then [0__x] is a member of A xor (x__1] is not a member of A.
- Please pay attention that if x is both belong and does not belong to A than we deal here with a non-local urelement (x € A and x not_€ A --> __)0____1 where 0__x is the side of the non-local urelement that exists in A (for example { 0__}_1 where [0__x] is in A) and [x_1] is the side of the non-local urelement 0____1 that is not in A.
- In other words if x both belongs and does not belong to A than you have to define first non-locality in the basis of Fuzzy-logic.
- Furthermore,if x is an intermediate state between locality (for example: each R member) and non-locality (the real-line itself, which in my system is a non-local urelement), than please show me the non-local urelement, that stands in the basis of Fuzzy-Logic.
- If you cannot find it in Fuzzy-Logic framework, then Fuzzy-Logic is based on a non-local urelement as its hidden assumption (it uses it without defining it).
- Since non-locality is not used in Fuzzy-Logic, and x is a local member of R set that cannot be both in and out of a given domain (where the domain is a memberships' degree) then by Fuzzy-logic the membership of x is [0,x] xor (x,1].
- Another example: Since each R member is a local object, then in the case of 50% membership, x= [0__50%] a member of A xor (50%__100%] not a member of A.
- Again, x is 50% a mamber of a and 50% not a member of A only if R is a non-local urelement (which is not true because R is a totally orderd collection of local objects that can be "in" xor "out" A).
- If R is a collection, then no one of its members (where each member is a one-of-meny object) can be both "in" and "out" A (which is a property that belongs only to a non-local urelement, which is not a one-of-many object).
- No. While certainly numbers are either elements of the set (or collection, if you prefer) of reals, let's have a look at another example more suited to the peculiarities of fuzzy logic. Let A be the set of rainy days. Is "September 16, 2006" an element of that set? Well, since (at least here) the weather is extremely good and dry, I would say: "Certainly not!", and "September 16, 2006" is a element of A with a certainty of 0. Now if we had some light showers today, I'd probably say: "Somewhat rainy, but not much.", and the certainty of "September 16, 2006" being an element of A would be, say, 0.3. Then the certainty of "September 16, 2006" not being an element of A would of course be 0.7. Thus, a day can be both somewhat rainy and somewhat not rainy. The only requirement is that its "rainyness" and "non-rainyness" add up to 1. But in no way are intervals like [0, 0.3] or [0.3, 1] elements (or members) of the set of rainy days - they aren't days at all.
- Fuzzy logic does not primarily concern itself with sets, elements, collections or memberships, but with statements and their truth or falseness. Sets only become relevant when I consider statements of the type "x is an element of set A", and assign them some level of truth. --Huon 14:06, 16 September 2006 (UTC)
Collections and urelements
You write:
- I agree that an urelement is not a set (by definition), but why then should it have "parts"?
My answer:
- If an object is defined by clearly distinct sub-objects that belong xor do not belong to it, then this object depends on the Collection concept. A set is a special case of a collection, where redundancy and order are ignored.
- A urelement is not related directly (as a non-empty set does) or indirectly (as the empty-set does) to the Collection concept, or in other words it is a non-composed (atomic) mathematical object.
You write:
- What is a "part" of an element?
My answer:
- If R is a non-empty set, then each real-number is a distinct part of it.
- Since a urelemet is not related to the Collection concept, it is not composed of members as R set does, or in other words, it is an atomic object.
- At the moment that you understand it, then you can start to understand my framework.
- In general, I find that you still unable to grasp a mathematical universe which its foundations are not based only on the Collection concept.
- My universe is based on a relation called bridging between a Collection of local elements ("in" xor "out" A) and a non-local urelement ("in" and "out" A).
- Bridging (notated by €) expands the memberships' concept beyond the standard membership, because the local and the non-local are not defined by each other (they are mutually independent).
- On the contrary, in the case of Set/Mamber membership, these concepts are defined by each other.
- The latter part of this answer is concerned with both non-locality and urelements, but I didn't want to cut it apart.
You write:
- why should "a collection of elements ordered by some rule" be "a property of a non-local urelement"?
My answer:
- This is an example of how you try to understand a non-local urelement in terms of a collection.
- Again, a non-local urelement is not a collection (it is not a one-of-many object), so "a collection of elements ordered by some rule" is NOT "a property of a non-local urelement".
- Thanks, I believe I have now understood your concept of collections. But I disagree with the lack of a relation between collections and urelements: An urelement is precisely an object which is not a collection. So in effect, the class of all objects (that's too large to be a set) is completely divided in those which are collections and the set (yes, this time it is a set) of those elements which are not collections themselves - the urelements. That's a little different from the standard definition of urelement (usually, urelements are those elements which are not sets, without any mention of the more general collections), but it's fine with me. And we have what you would call an xor relation between collections and urelements: Any given element x is either a collection or an urelement, but not both.
- It may be that for you, an element may be a "member" of another element without that other element being a collection, but then what's the difference between that element and the collection of its members? --Huon 14:06, 16 September 2006 (UTC)
Non-locality and the reals
You write:
- The law doesn't only say "P xor not-P", it says this statement is true
My answer:
- Indeed it is true only if not both "P and not-P" are true (which is the logical basis of locality).
You write:
- In general, I'm surprised about your use of the "real line". You surely know that in standard mathematics, the real numbers are the result of a long-winded construction, starting with the natural numbers and evolving through the integers and the rationals. In effect, real numbers usually are equivalence classes of Cauchy sequences of elements of the quotient field of the Grothendieck group (which happens to be a ring) of the natural numbers. Does this construction still work in your framework?
My answer:
- Yes, R set is the special case of a totally broken symmetry in my framework, where the Symmetry concept is a first-order property of my framework.
- In other words, my universe is a complementary relation between independent logical states that define locality and non-locality as the fundamental states of this universe.
You write:
- The relation "less than" is usually only defined on numbers, especially on real numbers.
My answer:
- In my system 0__0.kkk... [base n] < 0____1 means that the non-local number 0__0.kkk... cannot reach the completeness of the non-local urelement 0____1
- 0__0.kkk... is an intermediate state between locality (for example: each R member) and non-locality (the real-line itself, which in my system is a non-local urelement)
- In other words |R|(which is no more than a collection) < |Real-line| (which is not less than a non-local urelement) in my system.
You write:
- Shouldn't you instead construct "organic reals" out of organic natural numbers? If so, how precisely? Are the "organic reals" ordered? Are even the organic natural numbers ordered?
My answer:
- Since symmetry is used as a first-order property of my system, than my number system is based on any symmetrical state that can be found between parallel total symmetry and serial total broken symmetry.
- In this framework, Uncertainty and Redundancy are used as first-order properties of my number system.
- The standard framework is based only on totally broken symmetry. In order to see it, take for example Peano axioms. By this axiomatic system any natural number is at least both a cardinal and an ordinal.
- In my system each organic-natural-number is a cardinal but not immediately an ordinal.
- As a result, each given quantity has an non-empty inner-space between parallel symmetry and broken serial symmetry, which does not exist in the standard framework that is based only on a broken serial symmetry as a first-order property of the Set concept and the Number system that is based on it.
You write:
- Why shouldn't the statement "0.999... is an element (or, if you prefer, a member) of the set of numbers less than 1" also be both true and false at the same time? I read your answer, but could not understand it.
My answer:
- You still try to understand my system only in the terms of a collection, and if you do that most of what I say will be a gebberish to you.
- My system is the mathematical space that exists between the collection concept (which is based on a one-of-many element or a local element) and a non-local urelement (which is not a one-of-meny element).
- The logical basis of locality is based on "in" xor "out" membership, and the logical basis of non-locality is based on "in" and "out" membership.
- "In" and "out" membership cannot be undestood from the collection-only ("in" xor "out") point of view, and "in" xor "out" cannot be understood from a non-collection-only ("in" and "out") point of view.
- My system can be understood as a complementary relation between ("in" and "out") and ("in" xor "out"), where each side both prevents and complements the products of the other side (as can be seen in the case of the non-local numbers, which are the product of both locality and non-locality. From one hand a non-local number is a one-of-many object, so it is a member of a set, but from the other hand, its exact location on the real-line (the real-line in my system is not a collection, but it is a non-local urelement) does not exist).
- Please look again at figures 5 and 6:
Figure 5
Figure 5 illustrates a proof that the number 0.111… is not a representation of the number 1 in base 2, but the non-local number 0.111… < 1. Are there any numbers between 0.111… and 1? Yes, for any given base n>2, the non-local number 0.kkk… where k=n-1. For example:
Figure 6
Figure 6 demonstrates that between any given pair of R members, which are local numbers, there exists a non-local number, whose exact location on the real line does not exist. A local number is not a limit of any non-local number, because local and non-local numbers are mutually independent. Furthermore, no set of infinitely many elements can reach the completeness of a non-local urelement. Thus, any non-finite set is an incomplete mathematical object, when compared to a non-local urelement.
DoronSahdmi 22:33, 15 September 2006 (UTC)
- Thanks for your detailed answers. I sorted them by topic, so we may have a little more clarity. I answered the fuzzy logic remarks and those about the nature of connections (which were especially helpful) directly with those sections. Here I'll answer just the non-locality, which is still rather unclear to me.
- First of all, the law of contradiction says that P and not-P can never be true at the same time, whatever the statement P is. The fuzzy version (see above) of this law says that the degrees of certainty of P and not-P have to add up to 1. If this law does not hold any longer, then you must define something like "non-local statements", which may be true and false at the same time. How can one tell wether any given statement is local or non-local?
- While I have no problems with local objects, be they collections or urelements, I am still baffled by non-locality. Let me try a definition and tell me whether you agree:
Let x be an object. x is called non-local if there exists some object A such that x is a member of A and x is not a member of A at the same time.
That's how I understood definition 7. Here non-locality is a property of objects, not statements. Now let's have a look at a basic example: The real line. That should be a non-local object. For this example, what are x and A? is x the real line? Did I get it wrong, and A is the real line? What is the object which isn't the real line? Yours, Huon 14:06, 16 September 2006 (UTC)
Your write (please next time do not write your replies in different places along our dialog, because it is hard to find tham, thanks):
- Fuzzy logic does not primarily concern itself with sets, elements, collections or memberships, but with statements and their truth or falseness. Sets only become relevant when I consider statements of the type "x is an element of set A", and assign them some level of truth. --Huon 14:06, 16 September 2006 (UTC)
My answer:
- Ho, yes it does, by using Membership function (mathematics) and without it Fuzzy-Logic does not exist.
- You use the term "up to 1" as the basis of x = (0.3(belongs) and 0.7(does not belong)), and without it, the and connective is miningless, because if x both belongs and does not belong to A than you have to define first non-locality in the basis of Fuzzy-logic (and the 1 of the term "up to 1" cannot be but a non-local urelement).
- Furthermore, if x is an intermediate state between locality (for example: each R member) and non-locality (the real-line itself, which in my system is a non-local urelement), than please show me the non-local urelement, that stands in the basis of Fuzzy-Logic (for example, please look at figure 5 and see that a non-local number is the product of the relations between locality and non-locality, and so is a partial membership, but Fuzzy-Logic uses non-locality as an hidden assumption in order to work, where I clearly dafine non-locality in my framework).
- If you cannot find it in Fuzzy-Logic framework, then Fuzzy-Logic is based on a non-local urelement as its hidden assumption (it uses it without defining it).
- Since non-locality is not used in Fuzzy-Logic, and x is a local member of R set that cannot be both in and out of a given domain (where the domain is a memberships' degree) then by Fuzzy-logic the membership of x is [0,x] xor (x,1].
You write:
- First of all, the law of contradiction says that P and not-P can never be true at the same time, whatever the statement P is. The fuzzy version (see above) of this law says that the degrees of certainty of P and not-P have to add up to 1. If this law does not hold any longer, then you must define something like "non-local statements", which may be true and false at the same time. How can one tell wether any given statement is local or non-local?
My answer:
- My system has two indepentent extreme logical states.
- In one side we have locality (x is "in" xor "out" A) and on the other hand we have non-locality (x is "in" and "out" A).
- A local x is no more than a one-of-many object (which is the building-block of any collection), where a non-local x is not less than not a one-of-many object (= the real-line itself, which is a non-local urelement in my framework).
- Now think. if non-locality does not exist, than there cannot be any interaction between local objects, and we cannot go beyond a collection of a one element at a time (each local object is totally disconnected from any other local object).
- If locality does not exist, then there cannot be an object beyond one, becaue all we have is a single non-local urelement.
- So if we want to "move" beyond one, we need an association between the local and the non-local.
- The Standard system (and also Fuzzy-Logic) using non-locality as a hidden assumption (using it without definig it), whwere my framework clearly defines it and uses it as one of its foundamental states.
You write:
- While I have no problems with local objects, be they collections or urelements, I am still baffled by non-locality. Let me try a definition and tell me whether you agree:
Let x be an object. x is called non-local if there exists some object A such that x is a member of A and x is not a member of A at the same time.
- That's how I understood definition 7. Here non-locality is a property of objects, not statements. Now let's have a look at a basic example: The real line. That should be a non-local object. For this example, what are x and A? is x the real line? Did I get it wrong, and A is the real line? What is the object which isn't the real line? Yours, Huon 14:06, 16 September 2006 (UTC)
My answer:
- By using "{" and "}" notations we actually define a system that is based on two basic states which are "in" "{" and "}" or "out" "{" and "}".
- A is "{" and "}" system and we which to define what objects can logicaly exist according to "in","out" terms.
- Definition 1:
- Let x be an object. x is called local if for any system A
- x is a member of A xor x is not a member of A.
- Definition 2:
- Let x be an object. x is called non-local if for any system A
- x is a member of A and x is not a member of A.
- By definition 1 we get a local object ( for example: {.} xor .{ } )
- By definition 2 we get a non-local object ( for example: _{_} )
- A local object is a one-of-many object (it can be a member of some collection).
- A non-local object is not a one-of-many object (it cannot be a member of some collection).
- In my system, the real-line is a non-local object.
- I'm sorry for the confusion, but I tried to sort our discussion by topic, because I found it rather difficult to keep track of our several topics at once.
- Concerning fuzzy logic: As the membership function article states, what such a function measures is the degree of truth of membership in that set. Fuzzy logic on its own is concerned with non-integral degrees of truth (that is, not just 0 or 1, "true" or "false"). By the way, the membership function article even gives an example for a fuzzy set where you should be hard-pressed to say which elements are members and which are not.
- Concerning locality: I believe I finally understand what you mean, but unfortunately that's not possible. If I understood "it cannot be a member of some collection" correctly, then a non-local object should especially be one which never is an element of a set - but no matter what an object A is and what properties it may have, I can always construct the set {A} which contains A as its only element.
- Besides, if those definitions 1 and 2 above are correct, you would have to prove that locality and non-locality are mutually exclusive. There might a priori be one system A1 such that x is a member of A1 xor x is not a member of A1, and another system A2 such that x is a member of A2 and x is not a member of A2 at the same time! Such a proof should be exceedingly difficult (if not impossible); I assume you just made a copy&paste errror with your definition 1 and meant that x is called local if for every system A x is a member of A xor x is not a member of A. Yours, Huon 19:10, 16 September 2006 (UTC)
You write:
- I assume you just made a copy&paste errror with your definition 1 and meant that x is called local if for every system A x is a member of A xor x is not a member of A.
My answer:
Thank you Huon, I corrected it to:
- Definition 1:
- Let x be an object. x is called local if for any system A
- x is a member of A xor x is not a member of A.
- Definition 2:
- Let x be an object. x is called non-local if for any system A
- x is a member of A and x is not a member of A.
You Write:
- Concerning fuzzy logic: As the membership function article states, what such a function measures is the degree of truth of membership in that set. Fuzzy logic on its own is concerned with non-integral degrees of truth (that is, not just 0 or 1, "true" or "false"). By the way, the membership function article even gives an example for a fuzzy set where you should be hard-pressed to say which elements are members and which are not.
My answer:
- You have missed the main agrument which is: If by Fuzzy-Logic any given membership degree is based on x/1 relation (0 <= x <= 1), than x/1 has an exact location along [0,1], so what do you mean by "you should be hard-pressed to say which elements are members and which are not."?
- If x = 0.5/1 than [0,0.5] is "in" xor (0.5,1] is "out" in the case of R set, or [0__0.5] is "in" and [0.5__1] is "out" in the case of
- { 0__}__1 , where 0____1 is a non-local urelement.
You write:
- Concerning locality: I believe I finally understand what you mean, but unfortunately that's not possible. If I understood "it cannot be a member of some collection" correctly, then a non-local object should especially be one which never is an element of a set - but no matter what an object A is and what properties it may have, I can always construct the set {A} which contains A as its only element.
My answer:
- In that case you still do not understand non-locality, because I clearly wrote that __ can be both a local {__} xor __{ }
- or a non-local _{_} urelement.
- At the moment that you write {_{_}} you get a local urelement. In other words, a non-local urelement exists only in the case of _{_}.
- In other words, there is a fine tuning between notion and notation in my framework, which I think is both logical and intuitive.
You write:
- Besides, if those definitions 1 and 2 above are correct, you would have to prove that locality and non-locality are mutually exclusive. There might a priori be one system A1 such that x is a member of A1 xor x is not a member of A1, and another system A2 such that x is a member of A2 and x is not a member of A2 at the same time! Such a proof should be exceedingly difficult (if not impossible).
My answer:
- I do not have to prove that locality and non-locality are mutually exclusive, because definitions 1 and 2 are axiomatic states of my system.
- If you do not agree with me, than try to show how a non-local urelement (not a one-of-many object) and a collection (which is based on one-of-many elements) are not mutually exclusive, by definition.
- I say more than that, I say that standard logic and also Fuzzy-logic use non-locality as an hidden assumption, where my system defines it before using it.
- Also I say that no mathematical system can "move" beyond a singleton, if it is not based on at least locality and non-locality.
- Let me give you an example:
- On a table there is a finite unknown quantity of identical beads > 1
- and we have:
- A) To find their sum.
- B) To be able to identify each bead.
- Limitation: we are not allowed to use our memory after we count a bead.
- By trying to find the total quantity of the beads (where each bead representing loclity) without using our memory (representing non-loclity, and you can imagine it as a piece of string) we find ourselves stuck in 1, so we need an association between non-locality and locality if we want to be able to find the bead's sum.
- Let's cancel our limitation, so now we know how many beads we have, for example, value 3.
- Let us try to identify each bead, but they are identical, so we will identify each of them by its place on the table.
- But this is an unstable solution, because if someone takes the beads, put them between his hands, shakes them and put them back on the table, we have lost track of the beads identity.
- Each identical bead can be the bead that was identified by us before it was mixed with the other beads.
- We shall represent this situation by:
- ((a XOR b XOR c),(a XOR b XOR c),(a XOR b XOR c))
- By notating a bead as 'c' we get:
- ((a XOR b),(a XOR b),c)
- and by notating a bead as 'b' we get:
- (a,b,c)
- We satisfy condition B but through this "process" we define a universe, which exists between non-locality and locality, and can be systematically explored and be used to make Math.
- What I have found through this simple cognition's_basic_ability_test is that ZF or Peano axioms are using non-locality as an hidden assumption, which ignore our memory as the non-local urelement that actually enables as to "move" beyond 1 and also to order objects.
- So by this simple thought experiment and by continue with this beads/string analogy, we can say that any n > 1 is at least a neckless (beads and a string, or locality and non-locality).
- If you disagree with me, than please explain how Peano can use the succesor concept, without using his memory as a non-local urelment.
Let us go back to the begining of this dialog, where I wrote:
Z is a place holder of the Context concept (Z is a non-local urelement).
A, B, C, ... are place holders of independent and self-consistent mathematical objects (axioms)(A,B,C are local urelements).
Z without A, B, C, ... is not an interesting mathematical framework.
If Z does not exist, than A, B, C, ... have nothing in common, and no axiomatic system of more than a single axiom can be found (logically, all we have is A xor B xor C xor ...)
For example:
A___B___C___...
1 xor 0 xor 0 xor ... --> true
0 xor 1 xor 0 xor ... --> true
0 xor 0 xor 1 xor ... --> true
...
So, without at least Z and (A xor B) complementation, no interesting mathematical framework can be found.
DoronSahdmi 20:30, 16 September 2006 (UTC)
- Concerning fuzzy logic and fuzzy sets once more: Let us take a concrete example, a fuzzy subset of the reals. Its membership function f is given by (that's the membership function of the article, a little translated and rescaled). Now is 1 an element of the set given by that membership function? Yes? No? Somewhat? How about 2?
- Concerning non-locality, I fear your notation is not as intuitive as you believe. Just to take your example: By definition 2, there should be some "system" A (although you avoided to define what a system is and how it differs from, say, a collection) such that our memory, as a non-local object, is both a member of A and not a member of A at the same time. What is that system? If that's too concrete an example, I can ask the same question for the real line.
- I also didn't understand whether a non-local object can be an element of a set or not. Could you clarify that? By the way, at the moment I write {_{_}}, I don't get an urelement, but a set (maybe one containing an urelement). Unless your definition of urelement differs from the standard one, there should be an important difference.
- I just saw your corrected definitions. I still am baffled, because there now could a priori be an element which is neither local nor non-local. I would construct such an element as follows: Let x be an element which is not local (whether or not it's an urelement should be irrelevant here; I don't care). Then by definition 1 there exists a system A1 such that x is both a member of A1 and not a member of A1. Now I want to show that x isn't non-local, either. All I have to do, by definition 2, is to construct a system for which x is not both a member and not a member. Let us consider a system A2 which doesn't have any members. Yes, that's an extremely boring system, and we won't be able to deduce much from it. But especially A2 is a system which doesn't have x both as a member and not as a member. Thus x is not non-local. Yours, Huon 23:09, 16 September 2006 (UTC)
You write:
- Now is 1 an element of the set given by that membership function? Yes? No? Somewhat? How about 2?
My answer:
- If our system is based on x, where 0 <= x <= 1, then x is a distinct value of the relation x/1. Now, if x is a member of R, then each member of it is a distinct (a point-like) object, and this kind of object cannot represent both a membership and not a membership in the domain of the membership function. As a result, x/1 (or [0,x]) represents "in" and its complement to 1 (x,1] represents "out" in the domain of the membership function.
- In other words, the domain of the membership function is [0,x]"in" xor (x,1]"out" if x is a R member.
You write:
- ...you avoided to define what a system is and how it differs from, say, a collection...
My answer:
- A system is any framework where at least concepts like "in" and "out" are researched.
- If "{" , "}" are used to represent a system, then we reseach what relations exist between {"in"} or { }"out".
- Locality is {"in"} xor { }"out" ( for example: {.} xor .{ } ).
- Non-locality is {"in"} and { }"out" ( for example: _{_} ).
You write:
- I also didn't understand whether a non-local object can be an element of a set or not. Could you clarify that?
My answer:
- A set is a system that is based only on local objects ( {"in"} xor { }"out" ), so _{_} ( {"in"} and { }"out" ) is beyond set's membership.
You write:
- By the way, at the moment I write {_{_}}, I don't get an urelement, but a set (maybe one containing an urelement).
My answer:
- Yes, you are right, {_{_}} is a set that includes a urelement in it, but this urelement is not a non-local urelement, because it is completely included "in" a set and considered as a one-of-many object.
You write:
- Let x be an element which is not local (whether or not it's an urelement should be irrelevant here; I don't care).
- Ho, you care a lot, because if x is non-local ( {"in"} and { }"out" ) than it must be a urelement.
You write:
- Then by definition 1 there exists a system A1 such that x is both a member of A1 and not a member of A1
My answer:
- Definition 1 (what you call definition 2, so please correct it) is related only to a local object , so if x is non-local you cannot say anything about it by definition 1 (what you cal definition 2 by mistake).
You write:
- All I have to do, by definition 2 (again, you mix between definition 1 and definition 2), is to construct a system for which x is not both a member and not a member. Let us consider a system A2 which doesn't have any members. Yes, that's an extremely boring system, and we won't be able to deduce much from it. But especially A2 is a system which doesn't have x both as a member and not as a member. Thus x is not non-local.
My answer:
- By your definition, x does not exit so you cannot say anything about it, (actually, you can say that x does not exist).
- Concerning fuzzy logic: I gave a membership function and asked if 1 and/or 2 were elements of the fuzzy subset of the set of real numbers defined by that membership function. That should have been something like a yes-or-no question (not quite, but almost). Unfortunately, you didn't treat it as such. I fail to understand what you mean by "x is a distinct value of the relation x/1". I didn't even use x except as a variable while defining the function. A "relation x/1" wasn't defined (by either you or me), and usually I would read x/1 as "x divided by 1", which is again x, and not a relation.
- Next, I would like to direct your attention to a contradiction: "_{_} [...] is beyond set's membership" seems to mean that _{_} cannot be an element of a set. But a few lines later, you agree that "{_{_}} is a set" - and its element, obviously, is _{_}.
- Then, I am surprised by the claim that "if x is non-local [...] than it must be a urelement." Is every non-local element an urelement? I thought that 0___0.9999... was a non-local element which wasn't an urelement?
- Finally, you seem to have gotten my construction of an object which is neither local nor non-local wrong. First, I wantet to have an object which is not local (that's not the same as being non-local!). Of course I have to check definition 1, because that's the one which tells me whether an object is local. In order not to be local, my object has to fail definition 1. Next, I wanted to show that my object isn't non-local, either, and for non-locality, I need definition 2.
- You concluded your answers with writing that I showed "x does not exit". I happen to agree: An object which is not local (i.e. does not satisfy definition 1) does not exist. But that renders your entire theory a little worthless, doesn't it? Yours, Huon 10:31, 17 September 2006 (UTC)
You write:
- A "relation x/1" wasn't defined (by either you or me), and usually I would read x/1 as "x divided by 1", which is again x, and not a relation.
My answer:
- x/1 is the ratio between x and 1. I understand the word ratio as a relation between objects.
You write:
- Next, I would like to direct your attention to a contradiction: "_{_} [...] is beyond set's membership" seems to mean that _{_} cannot be an element of a set.
My answer:
- Dear Huon, _{_} notates a non-local urelement that its proprty is to be beyond any given domain (and in this case the domain is called a set, where a set cannot be but empty xor non-empty with one-of-many elements).
- If _{_} is in a set (completely included in it), then {_{_}} is not a non-local urelement but a local urelement and a member of a set.
- Furthermore, if _{_} is completely not included in a set, then we actually ignore its non-locality (it is non-local iff it is both in and out a set).
You write:
- I thought that 0___0.9999... was a non-local element which wasn't an urelement?
My answer:
- 0___0.9999... is a non-local number (it is the result of the relations between locality and non-locality. In other words,0___0.9999... is a member of a set, but its exact location along the real-line (which is a non-local urelement) does not exist).
You have asked me:
- What is a "non-finite object upon non-finite scales of [base n] levels" supposed to be? What are the "levels" you speak of? And if, as you write, "0.kkk... [base n] is not an R member", how can you compare it to either 1 or 0___1? The relation "less than" is usually only defined on numbers, especially on real numbers.
My answer:
Since the place value [base n>1] method is actually a non-finite fractal, then 0.kkk... [base n] (n>1,k=n-1) is a single path along the scale-levels of a non-finite fractal (as can be clearly seen in the case of 0.111... [base 2]):
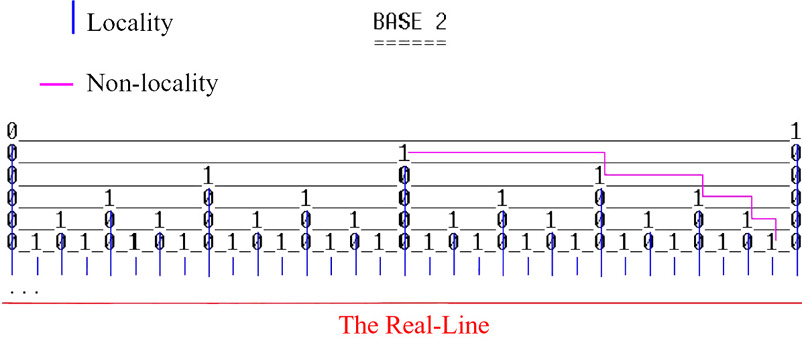
As can be clearly seen in the example, number 1 (which is a local number) is not the limit of the non-local number 0.111...[base 2], and as a result 0.111...[base 2] < 1.
- Now let us look again at your argument,
Here are the definitions:
- Definition 1:
- Let x be an object. x is called local if for any system A
- x is a member of A xor x is not a member of A.
- Definition 2:
- Let x be an object. x is called non-local if for any system A
- x is a member of A and x is not a member of A.
Your argument (part 1):
- I still am baffled, because there now could a priori be an element which is neither local nor non-local. I would construct such an element as follows: Let x be an element which is not local (whether or not it's an urelement should be irrelevant here; I don't care). Then by definition 1 there exists a system A1 such that x is both a member of A1 and not a member of A1.
My answer to part 1:
- If Not local is the nagation of xor connective, then in this case you use nxor (and as you see, we do not care if non-locality is nothing
- (0 0 -> T) or something (1 1 -> T) and all we care is that in is the same as out):
in out
0 0 -> T
0 1 -> F
1 0 -> F
1 1 -> T
Your argument (part 2):
- Now I want to show that x isn't non-local, either. All I have to do, by definition 2, is to construct a system for which x is not both a member and not a member. Let us consider a system A2 which doesn't have any members. Yes, that's an extremely boring system, and we won't be able to deduce much from it. But especially A2 is a system which doesn't have x both as a member and not as a member. Thus x is not non-local.
My answer to part 2:
- Not non-local is the nagation of nxor connective, so in this case you use xor, which its true table is:
in out
0 0 -> F
0 1 -> T
1 0 -> T
1 1 -> F
- In this case, all we care is that in is not the same as out (where in or out can be nothing or somthing).
- In order to get a true value in the case of 0-in 0-out non-locality, we have to use the nor connective, which its true table is:
in out
0 0 → T
0 1 → F
1 0 → F
1 1 → F
So non-locality is not based on an and connective (as I wrote in definition 2), but it is the nagation of xor, which is nxor, that its true table can be seen in part 1 of my answer.
THANK YOU VERY MUCH Huon, because your argument helped me to improve my theory.
The Membership concept needs logical foundations in order to be defined rigorously.
Let in be "a member of ..."
Let out be "not a member of ..."
Definition 1: A system is any framework which at least enables to research the logical connectives between in and out.
Let a thing be nothing or something.
Let x be a placeholder of a thing.
Definition 2: x is called local if for any system A, x is in A xor x is out A implies true.
The true table of locality is:
in out
0 0 → 0
0 1 → 1
1 0 → 1
1 1 → 0
Let x be nothing
Definition 3: x is called non-local if for any system A, x is in A nor x is out A implies true.
The true table of non-locality when x is nothing is:
in out
0 0 → 1
0 1 → 0
1 0 → 0
1 1 → 0
Let x be something
Definition 4: x is called non-local if for any system A, x is in A and x is out A implies true.
The true table of non-locality when x is something is:
in out
0 0 → 0
0 1 → 0
1 0 → 0
1 1 → 1
Let system Z be the complementation between non-locality and locality.
The true table of Z is:
in out
0 0 → 1
0 1 → 1
1 0 → 1
1 1 → 1
Let us return once more to Fuzzy-Logic:
If x=0 then x is not a member.
If 0 < x < 0.5 then x is mostly not a member.
If x=0.5 then x is equaly a member and not a member.
If 0.5 < x < 1 then x is mostly a member.
If x=1 then x is a member.
All these memberships are based on the proportion between x and 1, in system Z.
If the system is limited only to R members, then the proportion between x and 1 is distinct.
If non-local numbers are included, then the proportion between x and 1 is non-distinct.
A non-local number is the result of the complementary relations between locality and non-locality of system Z.
On a one hand it is a member of a set, but on the other hand its distinct location along the real-line (where the real-line is not a set, but it is a non-local urelement, in system Z) does not exist.
In system Z the non-local number 3.14...[base 10] < the local number pi, the non-local number 0.999...[base 10] < the local number 1 , etc.,..., etc.
- One final remark concerning fuzzy logic: You seem to identify an object which may or may not be an element of a fuzzy set with its image under the membership function. If that image is equal to 1, then the object is a member of the set, if that image is 0.5, the object is equally a member and not a member - the object itself need not be 1 or 0.5.
- Your revised version of non-locality looks much better to me, although it sill looks like work in progress to me.
- Concerning 0.9999..., I agree that you can define a non-local number which is a little less than 1 and call it 0.9999... (with good reason). But you will probably agree that's not what the 0.999... article speaks of: There a purely local number is considered, and that is also called 0.9999... (for other reasons). That local number cannot be your non-local 0.9999...<1; it can be shown to be equal to 1. Which of those numbers should be called 0.9999... is debatable, but the article happens to give the "mainstream" definition.
- If you don't mind, let us end this discourse here; it has grown rather long, and I'll probably archive it shortly. I would like to thank you for the interesting discussion; I learnt quite a lot about the foundations of set theory. Yours, Huon 09:45, 20 September 2006 (UTC)
- Dear Huon, The dialog with you is the best for me for the past 5 years, you are simply great.
- Last thing about Fuzzy-Logic.
- Let x be the urelement 0____1
- Let us look at |x| as a degree of cardinality of 0____1
- If |x|=0 then x is not a member ( notated by { }0____1 and x is a local urelement)
- If |x|=0.5 then x is equaly a member and not amember ( notated by { 0__}__1 and x is a non-local urelement )
- If |x|=1 then x is a member ( notated by {0____1} and x is a local urelement)
- Since non-locality does not exit in the framework of R, then 0.999...=1 in this framework.
- R is a partial case of my framework, which is the complementary relation between locality and non-locality.
- Have a good life dear Huon.


