Interferometria
La interferometria és la tècnica de combinar dues o més ones, de les quals es diu que interfereixen l'una amb l'altra. En termes d'equacions d'ona el patró d'interferència és un estat que depèn de l'amplitud i fase de totes les ones que contribueixen. Encara que el fenomen d'ona d'interferència és molt general, les aplicacions de la interferometria es poden utilitzar en una gran varietat de camps, incloent-hi astronomia, fibres òptiques, òptica, metrologia, estudis de mecànica quàntica com interferometria de neutrons i interferometria de neutrins i interferometria de teoria de cordes.[1][2]
Aquesta tècnica s'utilitza especialment en radioastronomia, essent més difícil la seva implementació en longituds d'ona més curta (visible). La principal raó és la precisió mecànica més gran que es requereix en utilitzar longituds d'ona més curta. En l'actualitat hi ha projectes ambiciosos d'interferòmetres òptics de gran escala combinant els feixos de llum de grans telescopis terrestres, com l'interferòmetre Keck a Hawaii i el Very Large Telescope Interferometer VLTI a Xile, mentre que entre els observatoris radioastronòmics es troben el Very Large Array (VLA) a EUA i l'Atacama Large Millimiter/submilliter Array (ALMA) a Xile.
En tots els casos el principi físic utilitzat és que dues ones de llum que coincideixen en fase s'amplifiquen mentre que dues ones en oposició de fase es cancel·len, i també hi ha qualsevol combinació intermèdia. Això permet mitjançant mesurament del grau de cancel·lació o amplificació de dos feixos làser, fer mesuraments de superfícies menors a la longitud d'ona. La interferometria no només es fa servir en astronomia; existeixen usos més comuns com el mesurament de curvatura de lents i miralls, així com la identificació de defectes tant en la superfície com en la composició. Per a aquestes aplicacions es poden utilitzar diferents tipus d'interferòmetres, com ara l'interferòmetre Twyman-Green i l'interferòmetre de Fizeau, entre molts d'altres.
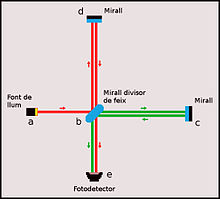
Un dels primers usos de la interferometria va ser en el famós experiment de Michelson i Morley (1887), que va demostrar la inexistència de l'èter, proporcionant les primeres evidències experimentals en les quals més tard s'asseuria la relativitat especial. En l'actualitat, interferòmetres similars al de Michelson es construeixen en grans instal·lacions (vegeu LIGO o VIRGO) en un intent de detectar ones gravitatòries, una conseqüència de la teoria de la relativitat general. L'11 de febrer del 2016, investigadors del LIGO van confirmar la detecció d'ones gravitacionals, observades per primera vegada el setembre del 2015.
Interferòmetre
[modifica]Un interferòmetre treballa sobre el principi que si dues ones que coincideix en la mateixa fase s'amplificaran l'una a l'altra mentre dues ones que tenen fases oposades es neutralitzaran, suposant que les dues tenguin la mateixa amplitud. En el començament, la majoria dels interferòmetres utilitzaven fonts de llum blanca (p. ex. l'experiment de la doble escletxa de Young de 1805). Avui dia els investigadors sovint utilitzen fonts de llum monocromàtica com làsers, i fins i tot el caràcter d'ona de matèria (dualitat ona-partícula) es pot explotar per construir interferòmetres. Un dels primers exemples d'interferòmetres de matèria fou l'interferòmetre d'electrons, més tard es construirien interferòmetres de neutrons. Al voltant de 1990 fou construït el primer interferòmetre d'àtoms, que seria seguit per interferòmetres de molècules. Actualment no és clar encara quina podria ser la màxima mida d'una partícula que es podria fer interferir amb una altra.
Les imatges astronòmiques de més alta resolució es produeixen utilitzant interferòmetres (a longituds d'ona tant òptiques com de ràdio). Per realitzar imatges interferomètriques en astronomia òptica s'exigeixen com a mínim tres telescopis (encara que és preferible usar-ne més). Aquesta tècnica també és útil per a la radioastronomia, que és el camp on primer es va aplicar.
Categories
[modifica]Els interferòmetres i les tècniques interferomètriques es poden categoritzar segons els criteris següents:
Detecció homodina versus heterodina
[modifica]W la detecció homodina, la interferència es produeix entre dos feixos amb la mateixa longitud d'ona (o freqüència portadora). La diferència de fase entre els dos feixos provoca un canvi en la intensitat de la llum al detector. Es mesura la intensitat resultant de la llum després de barrejar aquests dos feixos, o s'observa o registra el patró de franges d'interferència.[3] La majoria dels interferòmetres discutits en aquest article cauen en aquesta categoria. La tècnica heterodina s'utilitza per (1) desplaçar un senyal d'entrada a un rang de freqüència nou i també (2) amplificar un senyal d'entrada feble (utilitzant un mesclador actiu). Un senyal d'entrada feble de freqüència f1 és barrejada amb una freqüència de referència forta f2 d'un oscil·lador local (OL). La combinació no lineal dels senyals d'entrada crea dos senyals nous, un corresponent a la suma de f1 + f2 de les dues freqüències, i l'altra és la diferència f1 − f2. Aquestes freqüències noves es denominen heterodines. En general, es desitja una de les noves freqüències, i l'altre senyal és filtrat i descartat del senyal de sortida. El senyal de sortida tindrà una intensitat proporcional al producte de les amplituds dels senyals d'entrada.[3]
L'aplicació més important i utilitzada de la tècnica heterodina és en el receptor superheterodí (superhet), inventat en 1917-18 per l'enginyer nord-americà Edwin Howard Armstrong i el francès Lucien Lévy. En aquest circuit, el senyal de radiofreqüència entrant procedent de l'antena es barreja amb un senyal procedent d'un oscil·lador local (LO) i es converteix mitjançant la tècnica heterodina en un senyal de freqüència fixa més baixa anomenada freqüència intermèdia (FI). Aquesta FI és amplificada i filtrada, abans de ser aplicada a un detector que extreu el senyal d'àudio, que s'envia a l'altaveu.[4] La detecció heterodina òptica és una extensió de la tècnica heterodina a freqüències més altes (visibles).[3]
Encara que la interferometria òptica heterodina sol fer-se en un únic punt també és possible fer-la de camp ampli.[5]
Doble camí versus camí comú
[modifica]
Un interferòmetre de doble trajectòria és aquell en què el feix de referència i el feix de mostra viatgen per trajectòries divergents. Alguns exemples són l'interferòmetre de Michelson, l'interferòmetre de Twyman-Green i l'interferòmetre de Mach-Zehnder. Després de ser pertorbat per la interacció amb la mostra sota prova, el feix de la mostra es recombina amb el feix de referència per crear un patró d'interferència que pot ser interpretat.[1]:13-22
Un interferòmetre de trajecte comú és una classe d'interferòmetre en què el feix de referència i el feix de la mostra viatgen pel mateix camí. La Fig. 4 il·lustra l'interferòmetre de Sagnac, el giroscopi de fibra òptica, l'interferòmetre de difracció puntual i l'interferòmetre de cisallament lateral. Altres exemples d'interferòmetre de trajecte comú són el microscopi de contrast de fase de Zernike, el Biprisma de Fresnel, el Sagnac de àrea zero i l'interferòmetre de placa de dispersió.[6]
Divisió del front d'ona versus divisió de l'amplitud
[modifica]Interferòmetres de divisió de front d'ona
[modifica]Un interferòmetre de divisió de front d'ona divideix un front d'ona de llum que emergeix d'un punt o d'una escletxa estreta (és a dir llum espacialment coherent) i, després de permetre que les dues parts del front d'ona viatgin per camins diferents, permet que es recombinin.[7] La Fig. 5 il·lustra l'experiment d'interferència de Young i el mirall de Lloyd. Altres exemples d'interferòmetre de divisió del front d'ona són el biprisma de Fresnel, el Billet Bi-Lens i l'interferòmetre de Rayleigh.[8]

El 1803, l'experiment d'interferència de Young va jugar un paper important en l'acceptació general de la teoria ondulatòria de la llum. Si s'utilitza llum blanca en l'experiment de Young, el resultat és una banda central blanca d'interferència constructiva que correspon a una longitud de trajectòria igual des de les dues escletxes, envoltada per un patró simètric de franges de color d'intensitat decreixent. . A més de la radiació electromagnètica contínua, l'experiment de Young s'ha fet amb fotons individuals,[9] amb electrons,[10][11] i amb molècules buckyball prou grans per a ser vistes amb un microscopi electrònic.[12]
El mirall de Lloyd genera franges d'interferència combinant la llum directa d'una font (línies blaves) i la llum de la imatge reflectida de la font (línies vermelles) d'un mirall mantingut en incidència rasant. El resultat és un patró asimètric de franges. La banda de la mateixa longitud de trajectòria, més propera al mirall, és més fosca que brillant. El 1834, Humphrey Lloyd va interpretar aquest efecte com una prova que la fase d'un raig reflectit a la superfície frontal s'inverteix.[13][14]
Inferòmetres d'amplitud dividida
[modifica]
Un interferòmetre de divisió d'amplitud utilitza un reflector parcial per dividir l‟amplitud de l'ona incident en feixos separats que se separen i recombinen.
L'interferòmetre de Fizeau es mostra tal com es podria muntar per provar un pla òptic. Es col·loca un pla de referència exactament calculat sobre el pla que s'està provant, separat per estrets espaiadors. El pla de referència està lleugerament bisellat (només cal una fracció de grau de bisellat) per evitar que la superfície posterior del pla produeixi franges d'interferència. La separació dels plans de prova i de referència permet inclinar els dos plans entre ells. Ajustant la inclinació, que afegeix un gradient de fase controlat al patró de franges, es pot controlar l'espaiat i la direcció de les franges, de manera que es pot obtenir una sèrie de franges gairebé paral·leles fàcil d'interpretar en lloc d'un complex remolí de línies de contorn. No obstant això, per separar les plaques cal col·limar la llum que les il·lumina. La Fig 6 mostra un feix col·limat de llum monocromàtica que il·lumina les dues plaques i un divisor de feix que permet veure les franges a l'eix.[15][16]
L'interferòmetre de Mach-Zehnder és un instrument més versàtil que l'interferòmetre de Michelson. Cadascuna de les trajectòries de llum ben separades es recorre només una vegada, i les franges poden ajustar-se de manera que es localitzin en qualsevol pla desitjat.[1]:18 Normalment, les franges s'ajusten perquè se situïn al mateix pla que l'objecte de prova, de manera que les franges i l'objecte de prova es puguin fotografiar junts. Si es decideix produir franges amb llum blanca, aleshores, atès que la llum blanca té una longitud de coherència limitada, de l'ordre de micròmetre, cal tenir molta cura per igualar els camins òptics o no es veuran les franges. Com s'il·lustra a la Fig. 6, es col·locaria una cèl·lula de compensació en la trajectòria del feix de referència per igualar la cèl·lula de prova. Observeu també l'orientació precisa dels divisors de feix. Les superfícies reflectores dels divisors de feix s'orientarien de manera que els feixos de prova i de referència travessessin una quantitat igual de vidre. En aquesta orientació, els feixos de prova i de referència experimenten cadascun dues reflexions a la superfície frontal, cosa que resulta en el mateix nombre d'inversions de fase. El resultat és que la llum que recorre un camí òptic igual als feixos de prova i referència produeix una franja de llum blanca d'interferència constructiva.[17][18]
El cor de l'interferòmetre Fabry-Pérot és un parell de plans òptics de vidre parcialment platejats, separats per diversos mil·límetres o centímetres, amb les superfícies platejades enfrontades. (Com a alternativa, un etaló de Fabry-Pérot utilitza una placa transparent amb dues superfícies reflectants paral·leles.)[1]:35-36 Igual que a l'interferòmetre de Fizeau, les planxes estan lleugerament bisellades. En un sistema típic, la il·luminació és proporcionada per una font difusa col·locada al pla focal d'una lent col·limadora. Una lent d'enfocament produeix el que seria una imatge invertida de la font si els plans aparellats no hi fossin, és a dir, en absència dels plans aparellats, tota la llum emesa des del punt A que passa pel sistema òptic s'enfocaria al punt A'. A la Fig. 6, només es traça un raig emès des del punt A de la font. A mesura que el raig passa a través dels plans aparellats, es reflecteix de forma múltiple per produir múltiples raigs transmesos que són recollits per la lent d'enfocament i portats al punt A' a la pantalla. El patró d'interferència complet pren l'aparença d'un conjunt d'anells concèntrics. La nitidesa dels anells depèn de la reflectivitat dels plans. Si la reflectivitat és alta, donant lloc a un factor Q alt (és a dir alta finesa), la llum monocromàtica produeix un conjunt d'anells estrets i brillants contra un fons fosc.[19] A la Fig. 6, la imatge de baixa finor correspon a una reflectivitat de 0,04 (és a dir, superfícies sense depurar) front a una reflectivitat de 0,95 per a la imatge d'alta finesa.
La Fig. 6 il·lustra els interferòmetres Fizeau, Mach-Zehnder i Fabry-Pérot. Altres exemples d'interferòmetres de divisió d'amplitud són el Michelson, el Twyman-Green, l'interferòmetre de trajectòria desigual del làser i l'interferòmetre de Linnik.[20]
Vegeu també
[modifica]Referències
[modifica]- ↑ 1,0 1,1 1,2 1,3 Hariharan, P. Basics of Interferometry. Elsevier Inc., 2007. ISBN 0-12-373589-0.
- ↑ Bunch, Bryan H; Hellemans, Alexander. The History of Science and Technology. Houghton Mifflin Harcourt, April 2004, p. 695. ISBN 978-0-618-22123-3.
- ↑ 3,0 3,1 3,2 Paschotta, Rüdiger. «Detección heterodina óptica». RP Photonics Consulting GmbH. [Consulta: 1r abril 2012].
- ↑ Poole, Ian. «El superhet o receptor de radio superheterodino». Radio-Electronics.com. [Consulta: 22 juny 2012].
- ↑ Patel, R. «Interferometría heterodina de campo ancho utilizando una cámara de luz modulada CMOS personalizada». Optics Express, vol. 19, 24, 2011, pàg. 24546-24556. Bibcode: 2011OExpr..1924546P. PMID: 22109482.
- ↑ Mallick, S.; Malacara, D. «Common-Path Interferometers». A: Optical Shop Testing, 2007, p. 97. ISBN 9780470135976.
- ↑ Verma, R. K.. Optica de ondas. Discovery Publishing House, 2008, p. 97-110. ISBN 978-81-8356-114-3.
- ↑ «Dispositivos interferenciales - Introducción». OPI - Optique pour l'Ingénieur. [Consulta: 1r abril 2012].
- ↑ Ingram Taylor, Sir Geoffrey «Franjas de interferencia con luz débil». Proc. Camb. Phil. Soc..
- ↑ Jönsson, C «Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten». Zeitschrift für Physik. Bibcode: .161..454J 1961ZPhy. .161..454J.
- ↑ Jönsson, C «Difracción de electrones en rendijas múltiples». American Journal of Physics, vol. 4, 1, 1974, pàg. 4-11. Bibcode: .42....4J 1974AmJPh. .42....4J.
- ↑ {{cite book |title=Fundamental Physics - Heisenberg and Beyond: Simposio del centenario de Werner Heisenberg "Desarrollos en la física moderna" |fecha=2004 |editor=Springer |isbn=978-3540202011 |capítulo-url=https://books.google.cat/books?id=oLMCFnkFIdoC&pg=PA35%7Cautor1=Arndt, M. |autor2=Zeilinger, A. |capítulo=La incertidumbre de Heisenberg y la interferometría de ondas de materia con grandes moléculas |editor1=Buschhorn, G. W. |editor2=Wess, J.|páginas=35-52}
- ↑ Carroll, Brett. «pdf Simple espejo de Lloyd». American Association of Physics Teachers. [Consulta: 5 abril 2012].[Enllaç no actiu]
- ↑ Serway, R.A.. Principios de física: un texto basado en el cálculo, Volumen 1. Brooks Cole, 2010, p. 905. ISBN 978-0-534-49143-7.
- ↑ «Guideline for Use of Fizeau Interferometer in Optical Testing». NASA. Arxivat de l'original el 25 de septiembre de 2018. [Consulta: 8 abril 2012].
- ↑ «Dispositivos interferenciales - Interferómetro de Fizeau». Optique pour l'Ingénieur.. [Consulta: 8 abril 2012].
- ↑ Zetie, K.P.. «¿Cómo funciona un interferómetro Mach-Zehnder?». [Consulta: 8 abril 2012].
- ↑ Ashkenas, Harry I. El diseño y la construcción de un interferómetro Mach-Zehnder para su uso con el túnel de viento transónico GALCIT. Tesis de ingeniería. Instituto Tecnológico de California, 1950. DOI 10.7907/D0V1-MJ80.
- ↑ Betzler, Klaus. «edu.tr/~aykutlu/msn513/fibersensors/fabryperot.pdf Interferómetro Fabry-Perot». Fachbereich Physik, Universität Osnabrück. [Consulta: 8 abril 2012].[Enllaç no actiu]
- ↑ Nolte, David D. Interferometría óptica para biología y medicina. Springer, 2012, p. 17-26. ISBN 978-1-4614-0889-5.
