Königsberg'in Yedi Köprüsü

18. yüzyılda Königsberg ve 7 köprü

Königsberg'in yedi köprüsü; graf teorisinin temelini oluşturan ve XVIII. yüzyılda Königsberg köprülerinden ilhamlanılarak ortaya atılan ünlü bir matematik problemidir.

Problemin kökeni

Königsberg kentinde Eski Pregel ve Yeni Pregel nehirleri birleşerek Pregel (Pregolya) nehrini oluşturmaktadır. Bu nehirler, şehri dört bölüme ayırmaktadır ve nehir üzerinde bu bölgeleri birleştiren yedi köprü bulunmaktadır. Merak edilen ise şudur: Bütün köprülerden bir ve yalnız bir defa geçmek koşulu ile bir yürüyüş yapılabilir mi?

Bu soru, 1736'da İsviçreli matematikçi Leonhard Euler tarafından cevaplandırılmıştır.

Euler'in çözümü

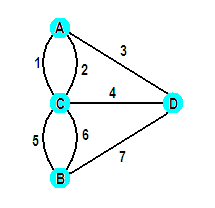
Aşağıdaki şekilde kara parçaları harflerle, köprüler ise sayılarla işaretlenmiştir. Önce çözümü biraz daha kolaylaştırmak ve şekli gereksiz bileşenlerden arındırmak amacıyla kara parçalarının noktalar, köprülerin ise bu noktaları birleştiren çizgiler olarak gösterildiği ikinci bir şekil yani graf (çizge) çizilir. Graflar graf elemanı, noktalar düğüm, düğüme bağlı olan elemanların sayısı ise düğüm derecesi olarak adladırılmak üzere soru, grafın herhangi bir düğümünden başlayarak yedi elemanının her birini bir ve yalnız bir kere kullanarak dolaşma problemine dönüşmüş olur.

→

1736'da Euler'in incelemeleri böyle bir gezintinin mümkün olmadığını kanıtlamış ve bu tür dolaşmayı mümkün kılacak grafların şu özelliklere sahip olmaları gerektiğini göstermiştir: Birleşik bir grafın bütün elemanlarını bir ve yalnız bir defa kullanarak dolaşmak için o grafın tek dereceli düğümlerinin sayısı eğer varsa iki olmalıdır. Tek dereceli düğümler dolaşmanın başlangıç ve bitiş düğümleridir. Grafta böyle düğümler yoksa dolaşmaya herhangi bir düğümden başlanabilir.

Çözümün temelinde yatan düşünce şudur: Bir düğüm, başlangıç ya da bitiş düğümü değilse o düğüme gelen kişinin turu tamamlayabilmek için oradan ayrılması gerekecektir. Dolayısıyla bu tip düğümler çift dereceleri olmalıdır. Oysa tek dereceli bir düğüme, örneğin D düğümüne ikinci kez gelen bir kişi çıkış yolu bulamayacaktır. Dolayısıyla bu düğüm ya gezintinin bitiş düğümü olmalıdır ya da başlangıç düğümü olarak seçilmelidir ki ikinci gelişte çıkış yolu bulunabilsin. Buna göre tek dereceli düğüm sayısı ikiden fazlaysa gezinti tamamlanamayacaktır.

Yürüyüşün sonunda başlangıç noktasına dönülebilmesi içinse bütün düğümler çift dereceli olmalıdır. Böylece, başlangıç ve bitiş düğümü aynı olan ve her bir elemanı sedece ve en az bir kez içeren turlara "Euler turu" ve Euler turu içeren graflara da "Euler grafları" denmiştir.

Problemin değişik biçimleri

Problemin, klasik ifadesinden farklı olarak her düğümün değişik renk veya isimlerle adlandırıldığı ve yeni köprülerin eklendiği çeşitleri de mevcuttur.^{İngilizce wikipedia}

Prensler ve Piskopos

Şehrin kuzey yakasında (A) Mavi Prens'in şatosu, güney yakasında (B) Kırmızı Prens'in şatosu, doğuda (D) Piskopos'un kilisesi ve ortadaki adada (C) bir han bulunmaktadır.

Mavi Prens köprülerden istenen şekilde yürünemeyeceğini anlar ve gizlice sekizinci köprüyü yapmayı planlar. Köprüyü öyle bir yere yapmalıdır ki akşamüstü kendi şatosundan yürüyüşe başlamalı ve gezintisini handa tamamlayarak zaferini kutlamalıdır. Ancak Kırmızı Prens gezintiyi tamamlayamamalıdır. Mavi Prens sekizinci köprüyü nereye inşa etmelidir?

Mavi Prens'in sekizinci köprüyü inşa etmesi Kırmızı Prens'i çok kızdırır. Handa tamamlayabileceği bir yürüyüşü olanaklı ve Mavi Prens'in yürüyüşünü imkânsız hale getirecek dokuzuncu köprüyü inşa etmek ister. Kırmızı Prens dokuzuncu köprüyü nereye inşa etmelidir?

Piskopos ise bu köprü kurma yarışını endişeyle izlemektedir. Bu durum hem şehrin görüntüsünü bozmaktadır hem de han da sonlanan yürüyüşler sarhoşluğu artırmaktadır. Tüm gezintilerin başladığı yerde bitmesi için onuncu bir köprü yaptırmalıdır. Onuncu köprü nereye inşa edilmelidir?

Çözüm

Öncelikle şekil düğümleri renkli (han → turuncu, kilise → beyaz) olan bir grafa indirgenir.

İlk soruda amaç orijinal çözümde de belirtildiği gibi tek dereceli düğümlerin sayının iki olmasını sağlamaktır. Tek dereceli düğümlerden biri başlangıç diğeri ise bitiş düğümü olacağına göre Mavi Prens'in sekizinci köprüyü kırmızı şato ile kilisenin arasına yapması gerekir. Böylece mavi ve turuncu düğümler tek dereceli kalarak başlangıç ve bitiş düğümleri olurlar.

Dokuzuncu köprünün inşasında da aynı yöntem izlenir. Bu kez yalnızca kırmızı ve turuncu düğümler tek dereceli kalmalıdır. Turuncu düğüm zaten tek derecelidir. Mavi düğümün çift dereceli, kırmızı düğümün ise tek dereceli olmasını sağlamak için dokuzuncu köprü mavi şato ile kırmızı şato arasına yapılmalıdır.

Renkli graf

Sekizinci köprü

Dokuzuncu köprü

Onuncu köprü

Piskopos'un isteğinde ise farklı bir durum söz konusudur. Yeni grafta başlangıç ve bitiş noktası aynı olmalıdır. Buna göre graftaki bütün düğümler çift dereceli yapılmalıdır. Dolayısıyla onuncu köprü kırmızı şato ile han arasına inşa edilmelidir.

Matematik tarihindeki önemi

Leonhard Euler’in bu araştırmaları matematikte tamamıyla yeni bir dal olan graf teorisinin ilk teoremi ve topolojinin keşfinin habercisi olmuştur. Çözümün ardından Euler, "Solutio problematis ad geometriam situs pertinentis" isimli makaleyi yayımlamıştır.

Çözümün kullanım alanları

Ayrıt rotalama problemleri, pek çok araştırmacının üzerinde çalıştığı bir rota en iyilemesi problemidir. Bu problemin, gerçek hayatta mektup dağıtımı, yol bakımı, kar temizleme, çöp toplama, devriye araçları ve yol tuzlama konularında pek çok uygulaması vardır. Gerek hükûmetler gerekse de işletmeler her yıl bu işlemler için önemli harcamalar yapmaktadırlar. Fakat planlamanın etkin olarak yapılamaması durumunda önemli miktarlarda kaynak israfı söz konusudur.

Köprülerin günümüzdeki durumu

Probleme konu olan yedi köprünün ikisi II. Dünya Savaşı sırasındaki bombardımanlarla yok edildi. Daha sonra iki tanesi Ruslar tarafından yıkıldı ve yerine modern bir otoyol inşa edildi. Geriye kalan üç köprü ise hala ayakta durmakta. Bunlardan biri Almanlar tarafından 1935 yılında tekrar inşa edildi. Sadece geri kalan ikisi Euler zamanından bu yana ayakta kalmayı başardı. Sonuç olarak günümüz modern Königsberg'inde beş köprü bulunmakta.

Graf teorisine göre günümüzde ikinci dereceden üç düğüm ve üçüncü dereceden iki düğüm olacak şekilde konumlanmış olan Königsberg'in köprülerinde her köprüden bir ve yalnız bir kez geçmek koşulu ile bir yürüyüş yapmak mümkündür. Fakat bu yürüş bir adada başlayıp diğer bir adada biteceğinden dolayı bir Euler Turu oluşturmamaktadır.

Dış bağlantılar

• Avriel, M. ve Golany, B. (1996). Mathematical Programming For Industrial Engineers, Marcel Dekker Inc., New York.
• Math Forum 11 Nisan 2008 tarihinde Wayback Machine sitesinde arşivlendi.
• Tokad, Y. (1996). Devre Analizi Dersleri, Çağlayan Kitabevi, İstanbul