توزیع گاما

گاما

تابع چگالی احتمال 325px|Probability density plots of gamma distributions
تابع توزیع تجمعی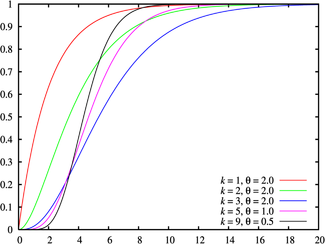
پارامترها	$k>0\,$ شکل (حقیقی) مقیاس (حقیقی) $\theta >0\,$
تکیه‌گاه	$x\in [0;\infty )\!$
تابع چگالی احتمال	$x^{k-1}{\frac {\exp {\left(-x/\theta \right)}}{\Gamma (k)\,\theta ^{k}}}\,\!$
تابع توزیع تجمعی	${\frac {\gamma (k,x/\theta )}{\Gamma (k)}}\,\!$
میانگین	$k\theta \,\!$
میانه	رابطه ساده صریح برای این پارامتر وجود ندارد
مُد	$(k-1)\theta {\text{ for }}k\geq 1\,\!$
واریانس	$k\theta ^{2}\,\!$
چولگی	${\frac {2}{\sqrt {k}}}\,\!$
کشیدگی	${\frac {6}{k}}\,\!$
آنتروپی	$k+\ln \theta +\ln \Gamma (k)\!$ $+(1-k)\psi (k)\!$
تابع مولد گشتاور	$(1-\theta \,t)^{-k}{\text{ for }}t<1/\theta \,\!$
تابع مشخصه	$(1-\theta \,i\,t)^{-k}\,\!$

توزیع گاما یکی از توزیع‌های احتمالی پیوسته است و دارای دو پارامتر مقیاس θ، و پارامتر شکل k می‌باشد. اگر k عددی طبیعی باشد آنگاه توزیع گاما معادل است با مجموع k متغیر تصادفی با توزیع نمایی با پارامتر ${\frac {1}{\theta }}$.

تعریف

تابع چگالی احتمال به صورت زیر محاسبه می شود:

$f(x;k,\theta )=x^{k-1}{\frac {e^{-x/\theta }}{\theta ^{k}\,\Gamma (k)}}\ \mathrm {for} \ x>0\,\,\mathrm {and} \,\,k,\theta >0.$

که در آن $\Gamma$ تابع گاما، θ پارامتر مقیاس، و k پارامتر شکل می‌باشند.

تابع گاما، انتگرالی همگراست و مقدار آن برابر با عددی مثبت است:

$\Gamma (k)=\int _{0}^{\infty }y^{k-1}.exp(-y)\,dy,k>0.$

ویژگی‌ها

هرگاه k (پارامتر شکل) یک عدد صحیح و مثبت چون n باشد، می‌توان از توزیع گاما برای تخمین زدن مدت‌زمان لازم برای روی‌دادن n پیشامد استفاده نمود.

توزیع مجموع

اگر $X_{i}\sim \Gamma \left(k_{i},\theta \right)$ اگر n متغیر دو به دو مستقل از هم باشند، آنگاه:

$\sum _{i=1}^{N}X_{i}\sim \Gamma \left(\sum _{i=1}^{N}k_{i},\theta \right)\,\!$

در نتیجه توزیع گاما بی‌نهایت تقسیم‌پذیر است.

توزیع‌های مرتبط

هرگاه k=۱ شود، حالت خاصی از توزیع گاما به وجود می‌آید که توزیع نمایی نامیده می‌شود. به ازای k=2 نیز توزیع گاما برابر توزیع رایلی میشود.

منابع

• مشارکت‌کنندگان ویکی‌پدیا. «Gamma distribution». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۱ فوریه ۲۰۰۸.
• اخوان نیاکی، دکتر سید تقی، نظریه احتمال و کاربرد آن (ویرایش دوم)، مؤسسهٔ انتشارات دانشگاه صنعتی شریف، صص 334 - 332، شابک ‎۹۷۸−۹۶۴−۷۹۸۲−۸۰−۱.