Bialjabar

Dalam matematika, sebuah bialjabar atas medan K adalah ruang vektor atas K yang merupakan unital aljabar asosiatif dan koasosiatif kounital koaljabar. Struktur aljabar dan koaljabar dibuat secara kompatibel dengan beberapa aksioma. Secara khusus, koperkalian dan kounit keduanya merupakan aljabar unital homomorfisme, atau ekuivalen, perkalian dan unital aljabar keduanya adalah morfisme coaljabar (pernyataan ini ekuivalen karena dinyatakan dengan diagram komutatif yang sama).

Bialjabar serupa dihubungkan oleh homomorfisme bialjabar. Homomorfisme bialjabar adalah peta linear yang merupakan aljabar dan homomorfisme koaljabar.

Sebagaimana tercermin dalam simetri diagram komutatif, definisi bialjabar adalah dual-diri, apabila mendefinisikan dual dari B (yang selalu dimungkinkan jika B adalah dimensi-hingga), maka secara otomatis merupakan bialjabar.

Definisi formal

(B, ∇, η, Δ, ε) adalah bialjabar atas K jika memiliki sifat-sifat berikut:

• B adalah ruang vektor atas K;
• peta linear-K (perkalian) ∇: B ⊗ B → B (dengan ekuivalen peta multilinear-K dari ∇: B × B → B) dan (satuan) η: K → B, sehingga (B, ∇, η) adalah asosiatif satuan aljabar;
• peta linear-K (komultiplikasi) Δ: B → B ⊗ B dan (kosatuan) ε: B → K, sehingga (B, Δ, ε) adalah (koasosiatif kounital) koaljabar;
• kondisi kompatibilitas yang dinyatakan oleh diagram komutatif sebagai berikut:

1. Perkalian ∇ dan perkalian Δ

   

   dimana τ: B ⊗ B → B ⊗ B adalah peta linear didefinisikan oleh τ(x ⊗ y) = y ⊗ x untuk semua x dan y di B,

2. Perkalian ∇ dan kosatuan ε

   1

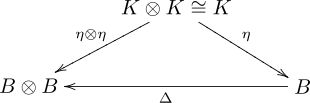
3. Koperkalian Δ and satuan η

   

4. Satuan η and kosatuan ε

   

Koasosiatif dan kosatuan

Peta linear-K dari Δ: B → B ⊗ B adalah koasosiatif jika $(\mathrm {id} _{B}\otimes \Delta )\circ \Delta =(\Delta \otimes \mathrm {id} _{B})\circ \Delta$.

Peta linear-K dari ε: B → K adalah satuan jika $(\mathrm {id} _{B}\otimes \epsilon )\circ \Delta =\mathrm {id} _{B}=(\epsilon \otimes \mathrm {id} _{B})\circ \Delta$.

Koasosiatifitas dan kosatuan dinyatakan dengan komutatifitas dari dua diagram berikut (kedua diagram tersebut merupakan kelipatan dari diagram yang menyatakan asosiasi dan unit aljabar):

Kondisi kompatibilitas

Empat diagram komutatif apabila dibaca dengan baik sebagai "perkalian dan satuan adalah homomorfisme aljabar" atau, secara ekuivalen, "perkalian dan satuan adalah homomorfisme bilangan bulat".

Pernyataan ini memiliki makna setelah menjelaskan struktur alami aljabar dan koaljabar untuk semua ruang vektor yang terlibat selain B: (K, ∇₀, η₀) adalah aljabar asosiatif unital dengan cara jelas dan (B ⊗ B, ∇₂, η₂) adalah aljabar asosiatif satuan dengan satuan dan perkalian multi

$\eta _{2}:=(\eta \otimes \eta ):K\otimes K\equiv K\to (B\otimes B)$

$\nabla _{2}:=(\nabla \otimes \nabla )\circ (id\otimes \tau \otimes id):(B\otimes B)\otimes (B\otimes B)\to (B\otimes B)$,

sehingga $\nabla _{2}((x_{1}\otimes x_{2})\otimes (y_{1}\otimes y_{2}))=\nabla (x_{1}\otimes y_{1})\otimes \nabla (x_{2}\otimes y_{2})$ atau, menghilangkan ∇ dan menulis perkalian sebagai penjajaran, $(x_{1}\otimes x_{2})(y_{1}\otimes y_{2})=x_{1}y_{1}\otimes x_{2}y_{2}$;

demikian pula, (K, Δ₀, ε₀) adalah jabar dengan cara yang jelas dan B ⊗ B adalah jabar dengan kosatuan dan koperkalian

$\epsilon _{2}:=(\epsilon \otimes \epsilon ):(B\otimes B)\to K\otimes K\equiv K$

$\Delta _{2}:=(id\otimes \tau \otimes id)\circ (\Delta \otimes \Delta ):(B\otimes B)\to (B\otimes B)\otimes (B\otimes B)$.

Maka, diagram 1 dan 3 mengatakan bahwa Δ: B → B ⊗ B adalah homomorfisme aljabar unital (asosiatif) (B, ∇, η) dan (B ⊗ B, ∇₂, η₂)

$\Delta \circ \nabla =\nabla _{2}\circ (\Delta \otimes \Delta ):(B\otimes B)\to (B\otimes B)$, atau hanya Δ(xy) = Δ(x) Δ(y),

$\Delta \circ \eta =\eta _{2}:K\to (B\otimes B)$, atau hanya Δ(1_B) = 1_{B ⊗ B};

diagram 2 dan 4 mengatakan bahwa ε: B → K is a homomorfisme aljabar unital (asosiatif) (B, ∇, η) dan (K, ∇₀, η₀):

$\epsilon \circ \nabla =\nabla _{0}\circ (\epsilon \otimes \epsilon ):(B\otimes B)\to K$, atau hanya ε(xy) = ε(x) ε(y)

$\epsilon \circ \eta =\eta _{0}:K\to K$, atau hanya ε(1_B) = 1_K.

Secara ekuivalen, diagram 1 dan 2 mengatakan bahwa ∇: B ⊗ B → B adalah homomorfisme dari (kounital koasosiatif) koaljabar (B ⊗ B, Δ₂, ε₂) dan (B, Δ, ε):

$\nabla \otimes \nabla \circ \Delta _{2}=\Delta \circ \nabla :(B\otimes B)\to (B\otimes B),$

$\nabla _{0}\circ \epsilon _{2}=\epsilon \circ \nabla :(B\otimes B)\to K$;

diagram 3 dan 4 mengatakan bahwa η: K → B adalah homomorfisme dari (kounital koasosiatif) koaljabar (K, Δ₀, ε₀) dan (B, Δ, ε):

$\eta _{2}\circ \Delta _{0}=\Delta \circ \eta :K\to (B\otimes B),$

$\eta _{0}\circ \epsilon _{0}=\epsilon \circ \eta :K\to K$,

dimana

$\epsilon _{0}=\epsilon \circ \eta$.

Contoh

Grup bialjabar

Contoh bialjabar adalah himpunan fungsi dari grup G (atau lebih umum, sembarang monoid) ke $\mathbb {R}$, yang dapat kita nyatakan sebagai ruang vektor $\mathbb {R} ^{G}$ yang terdiri dari kombinasi linear dari vektor basis standar e_g untuk setiap g ∈ G, apabila mewakili distribusi probabilitas atas G dalam kasus vektor semua koefisien non-negatif dan berjumlah 1. Contoh dari operator perkalian sesuai dan satuan yang menghasilkan kounital koaljabar adalah:

$\Delta (\mathbf {e} _{g})=\mathbf {e} _{g}\otimes \mathbf {e} _{g}\,,$

yang mewakili salinan variabel acak (apabila panjang ke semua $\mathbb {R} ^{G}$ dengan linearitas), dan

$\varepsilon (\mathbf {e} _{g})=1\,,$

(perluasan secara linear ke semua $\mathbb {R} ^{G}$) yang mewakili "menelusuri" variabel acak — yaitu, melupakan nilai variabel acak (diwakili oleh faktor tensor tunggal) untuk distribusi marjinal pada variabel yang tersisa (faktor tensor yang tersisa). Mengingat interpretasi (Δ,ε) dalam hal distribusi probabilitas seperti di atas, syarat konsistensi bialjabar sebesar kendala pada (∇,η) sebagai berikut:

1. η adalah operator distribusi probabilitas ternormalisasi yang independen dari semua variabel acak lainnya;
2. Produk ∇ memetakan distribusi probabilitas pada dua variabel ke distribusi probabilitas pada satu variabel;
3. Menyalin variabel acak dalam distribusi yang diberikan oleh η sama dengan memiliki dua variabel acak independen dalam distribusi η;
4. Mengambil produk dari dua variabel acak, dan salinan dari variabel acak yang dihasilkan, memiliki distribusi yang sama dengan menyiapkan salinan dari setiap variabel acak secara independen satu sama lain, dan mengalikannya secara berpasangan.

Sepasang (∇,η) yang memenuhi batasan ini adalah operator konvolusi

$\nabla {\bigl (}\mathbf {e} _{g}\otimes \mathbf {e} _{h}{\bigr )}=\mathbf {e} _{gh}\,,$

perluasan ke semua $\mathbb {R} ^{G}\otimes \mathbb {R} ^{G}$ dengan linearitas; ini menghasilkan distribusi probabilitas yang dinormalisasi dari distribusi pada dua variabel acak, dan memiliki distribusi delta $\eta =\mathbf {e} _{i}\;,$ dimana i ∈ G menunjukkan elemen identitas grup G.

Contoh lain

Contoh bialjabar lain termasuk aljabar tensor, apabila dibuat sebagai bialjabar dengan menambahkan perkalian dan satuan yang sesuai; ini bekerja secara rinci dalam artikel itu.

Bialjabar apabila diperluas ke aljabar Hopf, jika antipode yang sesuai dapat ditemukan. Jadi, semua aljabar Hopf adalah contoh bialjabar. Struktur serupa dengan kompatibilitas yang berbeda antara produk dan komultiplikasi, atau jenis perkalian dan perkalian yang berbeda, termasuk bialjabar Lie dan aljabar Frobenius. Contoh tambahan diberikan dalam artikel tentang koaljabar.

Lihat pula

• Kuasi-bialjabar

Referensi

• Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Șerban (2001), Hopf Algebras: An introduction, Pure and Applied Mathematics, 235 (edisi ke-1st), Marcel Dekker, ISBN 0-8247-0481-9 .