Condorcet-Paradoxon

Das Condorcet-Paradoxon oder Problem der zyklischen Mehrheiten (auch Wahlparadoxon, Zirkelpräferenz oder Schere-Stein-Papier-Prinzip) ist ein nach Marie Jean Antoine Nicolas Caritat, Marquis de Condorcet benanntes Paradoxon bei Wahlverfahren, das sich vor allem bei paarweisen Abstimmungen und Wahlen (Condorcet-Methode) auswirkt. Das sogenannte Paradoxe ist das Folgende: Das Abstimmungsergebnis bzw. die kollektive Präferenz/Entscheidung ist zyklisch, d. h. nicht transitiv, obwohl die individuellen Präferenzen transitiv sind. Dies kann so interpretiert werden, dass bei einer Agenda jede Mehrheitsentscheidung durch eine andere ersetzt wird. Daraus lässt sich folgern, dass es keinen Condorcet-Sieger gibt.

Grundaussage: Es ist möglich, dass eine Mehrheit die Option A gegenüber einer Option B bevorzugt, zugleich eine Mehrheit die Option B gegenüber einer Option C bevorzugt und dennoch eine Mehrheit die Option C gegenüber der Option A bevorzugt.

Dies ist dadurch möglich, dass jeder Wähler seine eigene Reihenfolge der Präferenzen hat. Teilen sich aber die Wahlmöglichkeiten in zwei entgegengesetzte Lager auf, deren Wahlmöglichkeiten nur schwächer oder stärker in diese Richtung gehen, tritt dieses Phänomen nicht auf.

Erläuterung

Graphische Darstellung eines Zirkelschlusses (Verletzung der Transitivitätsannahme) in einem 2-dimensionalen Präferenz-Raum: Die Wähler sind durch die blauen Punkte dargestellt, die Wahlmöglichkeiten durch die roten Punkte und die Präferenzreihenfolge durch die Pfeile. Die dargestellte zyklische kollektive Präferenz stellt eine Verletzung der Transitivitätsannahme dar.

→ Hauptartikel: Präferenzrelation

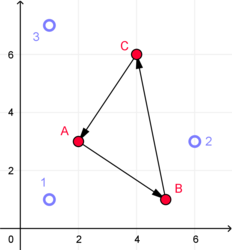
Wir nehmen an, es gebe drei rational handelnde Agenten: $x$, $y$ und $z$. $x$ hat dabei am liebsten Option $\mathrm {A}$, am zweitliebsten Option $\mathrm {B}$ und am wenigsten gern Option $\mathrm {C}$. $y$ hat am liebsten Option $\mathrm {B}$, dann Option $\mathrm {C}$ und zuletzt $\mathrm {A}$. Person $z$ schließlich hat die Wunschliste $\mathrm {C}$, $\mathrm {A}$, $\mathrm {B}$.

In Tabellenform:

	$x$	$y$	$z$
Erstwunsch	$\mathrm {A}$	$\mathrm {B}$	$\mathrm {C}$
Zweitwunsch	$\mathrm {B}$	$\mathrm {C}$	$\mathrm {A}$
Drittwunsch	$\mathrm {C}$	$\mathrm {A}$	$\mathrm {B}$

In formaler Schreibweise die Präferenzen:

• Für Agent $x$: $\;\mathrm {A} \;\succ \;\mathrm {B} \;\succ \;\mathrm {C}$.
• Für Agent $y$: $\;\mathrm {B} \;\succ \;\mathrm {C} \;\succ \;\mathrm {A}$.
• Für Agent $z$: $\;\mathrm {C} \;\succ \;\mathrm {A} \;\succ \;\mathrm {B}$.

Zwei von drei ($x$ und $z$) bevorzugen die Option $\mathrm {A}$ vor der Option $\mathrm {B}$. Zwei von drei ($x$ und $y$) bevorzugen auch die Option $\mathrm {B}$ vor der Option $\mathrm {C}$. Aber es gibt ebenfalls zwei ($y$ und $z$), die die Option $\mathrm {C}$ der Option $\mathrm {A}$ vorziehen (Zirkelschluss). Um eine gemeinsame Rangliste gemäß der Condorcet-Methode aufzustellen, müsste man also sowohl $\mathrm {A}$ vor $\mathrm {B}$ und $\mathrm {B}$ vor $\mathrm {C}$ als auch $\mathrm {C}$ vor $\mathrm {A}$ anordnen, denn im direkten Vergleich hat $\mathrm {A}$ vor $\mathrm {B}$, $\mathrm {B}$ vor $\mathrm {C}$ und $\mathrm {C}$ vor $\mathrm {A}$ die Mehrheit. Eine solche Rangliste ist aber nicht möglich.

Dies gilt natürlich auch, wenn $x$, $y$ und $z$ nicht nur jeweils eine Person, sondern (annähernd) gleich große Gruppen darstellen. Genauer gesagt, muss jede Gruppe lediglich kleiner sein als die beiden anderen zusammen.

Das Ergebnis ist folglich vom Abstimmungsleiter und dessen Wahl der Reihenfolge der Wahlvorgänge abhängig: Es sei die obige Situation gegeben, und sie sei dem Abstimmungsleiter bekannt. Dann kann er, wenn er selbst Alternative $\mathrm {A}$ bevorzugt, zunächst zwischen $\mathrm {B}$ und $\mathrm {C}$ abstimmen lassen: Hier gewinnt $\mathrm {B}$. Damit erklärt er $\mathrm {C}$ für ausgeschieden und lässt zwischen $\mathrm {A}$ und $\mathrm {B}$ abstimmen, wo nun $\mathrm {A}$ gewinnt. Es sieht nun so aus, als ob eine überwältigende Mehrheit hinter $\mathrm {A}$ stünde, schließlich hat dieses klar über $\mathrm {B}$ und $\mathrm {B}$ klar über $\mathrm {C}$ gesiegt. Eine Abstimmung zwischen $\mathrm {A}$ und $\mathrm {C}$, die gezeigt hätte, dass die Präferenz keineswegs klar ist, hat nicht stattgefunden.

Bedeutung

Die Sozialwahltheorie untersucht das Condorcet-Paradoxon und andere Aggregationsprobleme bei Abstimmungen und Wahlen. Das Condorcet-Paradoxon ist ein einfaches Beispiel dafür, dass sich aus mehreren individuellen transitiven Präferenzlisten ohne willkürliche Bevorzugung nicht immer kollektive transitive Präferenzlisten erstellen lassen. Insbesondere ist es ein Spezialfall des Unmöglichkeitssatzes von Arrow, der die prinzipielle Unmöglichkeit einer stets vorhandenen „demokratischen“ kollektiven Präferenzliste beweist. Dies wirft einige Fragen in der Demokratietheorie auf; insbesondere zeigt es nach Ansicht einiger, dass eine Demokratisierung von wirtschaftlichen oder politischen Entscheidungen nicht immer zu optimalen Ergebnissen führt. Doch wie häufig tauchen zirkuläre Präferenzen auf?

Ersetzen wir die abstrakten Variablen in der Tabelle durch konkrete Optionen in einer Sachentscheidung: Ein Gremium mit 3 Mitgliedern (Xaver, Yoshi, Zelda) berät über die Geschwindigkeitsbegrenzung auf einer Straße.

A = niedrigere Geschwindigkeit
B = die gegenwärtige Geschwindigkeit
C = höhere Geschwindigkeit

Lesen wir die Tabelle: Xaver will am ehesten die niedrigere Geschwindigkeit und am wenigsten die höhere. Yoshi möchte am ehesten den gegenwärtigen Kompromiss. Zelda mag am ehesten die höchste Geschwindigkeit, am zweitliebsten hat sie die niedrigste Geschwindigkeit. Die Präferenzen des Gremium-Mitglieds Zelda sind merkwürdig. Es kann immer vorkommen, dass die Präferenzen nicht transitiv sind. Man könnte nun denken, dass zirkuläre Mehrheiten bei eindimensionalen Entscheidungen praktisch nicht auftauchen. Das ist aber falsch. So könnte Zelda meinen, erkannt zu haben, dass bei niedriger Geschwindigkeit leichter gebremst werden kann, und bei hoher Geschwindigkeit ein Hormon ausgeschüttet werden würde, welches die Wachsamkeit erhöhen würde. Möglicherweise ist auf der Straße auch eine Gruppe von Ampeln, und nur bei höherer oder niedriger Geschwindigkeit können die Grünphasen ausgenutzt werden. Nur bei normaler Geschwindigkeit gebe es keinen Vorteil. Daraus folgt, dass zyklische Präferenzen durchaus möglich sind.

Entdeckung

Vermutlich als erster beschrieb Condorcet dieses Paradoxon in seinem Essai sur l’application de l’analyse à la probabilité des décisions rendues à la pluralité des voix (Paris 1785). Es geriet praktisch in Vergessenheit, bis Charles Lutwidge Dodgson und Edward John Nanson es in den 1870ern unabhängig voneinander wiederentdeckten. Danach geriet es erneut in Vergessenheit, bis Duncan Black und Kenneth Arrow es in den 1940ern bei ihren Untersuchungen unabhängig voneinander wiederentdeckten.

Literatur

• Jean-Antoine-Nicolas de Caritat Condorcet, marquis de: Essai sur l’application de l’analyse à la probabilité des décisions rendues à la pluralité des voix. Imprimerie royale, Paris 1785 (Volltext in der Google-Buchsuche). 
• William V. Gehrlein: Condorcet’s Paradox. Series: Theory and Decision Library C, Vol. 40. Springer, Berlin/Heidelberg 2006, ISBN 978-3-540-33798-0, doi:10.1007/3-540-33799-7.