Coordonnées cartésiennes

En coordonnées cartésiennes planaires, la position d'un point A est donnée par les distances x_A (abscisse à l'origine) et y_A (ordonnée à l'origine).

En coordonnées cartésiennes tridimensionnelles, la position d'un point P est donnée par les distances x, y et z.

Un système de coordonnées cartésiennes permet de déterminer la position d'un point dans un espace affine (droite, plan, espace de dimension 3, etc.) muni d'un repère cartésien. Le mot cartésien vient du mathématicien et philosophe français René Descartes.

Les coordonnées cartésiennes ont été inventées par René Descartes et Pierre de Fermat.

Il existe d'autres systèmes de coordonnées permettant de repérer un point dans le plan ou dans l'espace.

Abscisse sur une droite affine

Sur une droite affine $D$, un repère est la donnée de :

• une origine $O$, c'est-à-dire un point distingué de $D$ ;
• un vecteur ${\vec {v}}$ de la droite vectorielle directrice ${\vec {D}}$. Ce vecteur porte deux informations :
  • une orientation : un point $A$ est à droite de $O$ lorsque le vecteur ${\overrightarrow {OA}}$ est positivement colinéaire à ${\vec {v}}$ ;
  • une unité : un point $A$ est à la distance $r$ de $O$ lorsque ${\overrightarrow {OA}}=\pm r\cdot {\vec {v}}$.

Repère cartésien sur une droite.

Dans ce cas, l'abscisse du point $M$ est l'unique réel $r$ tel que : ${\overrightarrow {OM}}=r\cdot {\vec {v}}$.

Il y a donc une correspondance entre les points d'une droite affine et l'ensemble des réels.

On peut remarquer qu'il existe des systèmes de graduation non régulière mais le repère n'est plus appelé cartésien (voir échelle logarithmique).

Coordonnées cartésiennes dans le plan

Dans un plan affine, les coordonnées cartésiennes sont sans doute la manière la plus naturelle de définir un système de coordonnées. Un repère (cartésien) du plan affine $P$ est la donnée conjointe de :

• un point d'origine $O$.
• deux vecteurs ${\vec {i}}$ et ${\vec {j}}$ non colinéaires du plan vectoriel directeur ${\vec {P}}$.

Les axes de coordonnées sont les droites affines $(Ox)=(O,{\vec {i}})$ et $(Oy)=(O,{\vec {j}})$. Ces droites admettent des graduations respectives fournies par $O$ et les vecteurs ${\vec {i}}$ et ${\vec {j}}$.

représentation d'un repère dans un plan

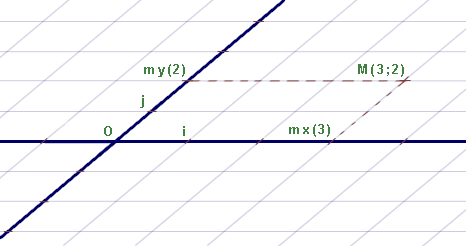
Par un point $M$, on est en droit de tracer :

• une droite parallèle à $(Oy)$ qui coupe $(Ox)$ en $m_{x}$ d'abscisse $x$, dans le repère $(O,{\vec {i}})$
• une droite parallèle à $(Ox)$ qui coupe $(Oy)$ en $m_{y}$ d'abscisse $y$ dans le repère $(O,{\vec {j}})$.

Le couple de réels $(x,y)$ est uniquement déterminé par le point $M$, on l'appelle les coordonnées de $M$ dans le repère $(O;{\vec {i}},{\vec {j}})$ :

• Le réel $x$ est appelé l'abscisse de $M$ ;
• Le réel $y$ est appelé l'ordonnée de $M$.

Réciproquement, à tout couple $(x,y)$, correspond un unique point $M$ de coordonnées d'abscisse $x$ et d'ordonnée $y$. C'est le point d'intersection des deux droites suivantes :

• La droite parallèle à $(Ox)$ passant par le point de $(Oy)$ d'abscisse $y$ ;
• La droite parallèle à $(Oy)$ passant par le point de $(Ox)$ d'abscisse $x$.

Cette construction peut être interprétée comme la mise en place d'un parallélogramme de sommets $O$ et $M$.

En termes vectoriels, on obtient l'identité suivante :

${\overrightarrow {OM}}=x{\vec {i}}+y{\vec {j}}$

Ce qui permet de faire une correspondance entre le calcul sur des coordonnées et le calcul vectoriel.

Cas de la base orthonormée

Les bases orthonormées n'ont de sens que dans les plans affines euclidiens. Dans un plan affine euclidien, une base $(O;{\vec {i}},{\vec {j}})$ est dit orthonormée lorsque les vecteurs ${\vec {i}}$ et ${\vec {j}}$ sont d'une part de longueur 1 (de norme 1) et d'autre part orthogonaux, c'est-à-dire que le produit scalaire des deux vecteurs est nul.

Autrement dit, les axes de coordonnées sont deux droites affines orthogonales avec le même système de graduation.

Repère orthonormé dans le plan.

Dans ce cas, on peut calculer des distances et des orthogonalités en utilisant le théorème de Pythagore. Voici un formulaire :

• Pour un point $M$ de coordonnées $(x,y)$, la distance $OM$ s'écrit :

$OM={\sqrt {x^{2}+y^{2}}}$

Dans le dessin ci-à droite, on a placé dans un repère orthonormé les points $A$ de coordonnées $(1,1)$ et $B$ de coordonnées $(4,5)$. Le calcul de la distance $AB$ est alors :

$AB={\sqrt {(4-1)^{2}+(5-1)^{2}}}=5$

• Les vecteurs ${\vec {u}}(x,y)$ et ${\vec {v}}(X,Y)$ sont orthogonaux si et seulement si $xX+yY=0$.

Le calcul des distances et des angles étant souvent un objectif de la géométrie plane euclidienne, on privilégie particulièrement les repères orthonormés. À tel point que certains ouvrages réservent le terme de coordonnées cartésiennes à ce type de repère, les autres coordonnées étant appelées coordonnées obliques.

Coordonnées cartésiennes dans l'espace

Le principe de construction sera le même. Dans un espace affine $E$ de dimension 3, un repère (cartésien) est la donnée conjointe de :

• un point d'origine $O$,
• et trois vecteurs non coplanaires ${\vec {i}}$, ${\vec {j}}$, et ${\vec {k}}$.

Les axes de coordonnées sont les droites affines concourantes $(Ox)=(O;{\vec {i}})$, $(Oy)=(O;{\vec {j}})$ et $(Oz)=(O;{\vec {k}})$.

Repère cartésien "oblique" dans l'espace.

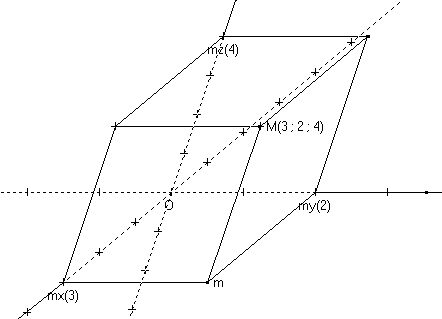
Pour un point $M$, on est en droit de tracer :

• un plan parallèle au plan $Oyz$ qui coupe $Ox$ en $m_{x}$ d'abscisse $x$ ;
• un plan parallèle au plan $Oxz$ qui coupe $Oy$ en $m_{y}$ d'abscisse $y$ ;
• un plan parallèle au plan $Oxy$ qui coupe $Oz$ en $m_{z}$ d'abscisse $z$.

Le triplet de réels $(x,y,z)$ est uniquement déterminé par la position du point $M$. Il s'appelle les coordonnées (cartésiennes) de $M$ dans le repère $(O;{\vec {i}},{\vec {j}},{\vec {k}})$ :

• le réel $x$ s'appelle l'abscisse ;
• le réel $y$ s'appelle l'ordonnée ou la profondeur ;
• le réel $z$ s'appelle la cote ou la hauteur.

Réciproquement, à tout triplet de réels $(x,y,z)$ correspond un unique point $M$ d'abscisse $x$, d'ordonnée $y$ et de cote $z$. Ce point s'obtient comme l'intersection :

• du plan parallèle au plan $Oyz$ passant par le point de $Ox$ d'abscisse $x$,
• du plan parallèle au plan $Oxz$ passant par le point de $Oy$ d'abscisse $y$ et
• du plan parallèle au plan $Oxy$ passant par le point de $Oz$ d'abscisse $z$.

Ces trois plans ainsi que les trois plans de bases $Oxy$, $Oxz$ et $Oyz$ dessinent un parallélépipède.

Il y a correspondance biunivoque entre tout point $M$ et tout triplet de réels appelés alors système de coordonnées de $M$.

De même que dans le plan, ces coordonnées se réinterprètent via l'écriture vectorielle :

${\overrightarrow {OM}}=x{\vec {i}}+y{\vec {j}}+z{\vec {k}}$

Repères orthonormés

Repère orthonormé dans l'espace.

Dans un espace affine euclidien de dimension 3, un repère $(O;{\vec {i}},{\vec {j}},{\vec {k}})$ est dit orthonormé lorsque les vecteurs ${\vec {i}}$, ${\vec {j}}$, et ${\vec {k}}$ sont unitaires et deux à deux orthogonaux. Cette deuxième condition s'écrit :

$\langle \mathbf {i} \mid \mathbf {j} \rangle =0$ ; $\langle \mathbf {j} \mid \mathbf {k} \rangle =0$ ; $\langle \mathbf {k} \mid \mathbf {i} \rangle =0$

Comme dans le plan, il sera nécessaire de prendre un repère orthonormé si l'on désire travailler sur des distances et des angles. La distance s'écrira alors :

$OM={\sqrt {x^{2}+y^{2}+z^{2}}}$

Coordonnées cartésiennes en dimension n

Les observations précédentes permettent de remarquer un lien entre couple ou triplet de réels et vecteurs du plan ou de l'espace. Ce lien se généralise à tout espace vectoriel ou affine de dimension finie sur un corps K.

Si $({\vec {e_{1}}},{\vec {e_{2}}},\dots ,{\vec {e_{n}}})$ est une base d'un espace vectoriel sur un corps K alors, pour tout vecteur ${\vec {v}}$, il existe un unique n-uplet $(x_{1},x_{2},\dots ,x_{n})\,$ élément de Kⁿ  tel que :

${\vec {v}}=x_{1}{\vec {e_{1}}}+x_{2}{\vec {e_{2}}}+\dots +x_{n}{\vec {e_{n}}}\,$ .

Ce n-uplet est appelé système de coordonnées cartésiennes du vecteur ${\vec {v}}$ dans la base $({\vec {e_{1}}},{\vec {e_{2}}},\dots ,{\vec {e_{n}}}$). La correspondance entre chaque vecteur et chaque n-uplet permet de construire un isomorphisme d'espaces vectoriels entre V et Kⁿ.

Pour travailler sur des systèmes de coordonnées de points, il suffit d'ajouter à la base précédente un point O appelé origine. Les coordonnées du point M étant celles du vecteur ${\overrightarrow {OM}}$.

Enfin, pour travailler sur des distances, il sera nécessaire de construire une base orthonormale (dans laquelle tous les vecteurs sont de norme 1 et chaque vecteur est orthogonal à tous les autres). La distance OM s'exprimera alors sous la forme suivante :

$OM={\sqrt {x_{1}^{2}+x_{2}^{2}+\dots +x_{n}^{2}}}\,$

Cinématique dans l'espace

Les quantités cinématiques, position, vitesse et accélération sont données par :

${\begin{aligned}{\overrightarrow {OM}}&=x{\overrightarrow {u_{x}}}+y{\overrightarrow {u_{y}}}+z{\overrightarrow {u_{z}}}\\{\dot {\overrightarrow {OM}}}&={\dot {x}}{\overrightarrow {u_{x}}}+{\dot {y}}{\overrightarrow {u_{y}}}+{\dot {z}}{\overrightarrow {u_{z}}}\\{\ddot {\overrightarrow {OM}}}&={\ddot {x}}{\overrightarrow {u_{x}}}+{\ddot {y}}{\overrightarrow {u_{y}}}+{\ddot {z}}{\overrightarrow {u_{z}}}\\\end{aligned}}$

Coordonnées cartésiennes dans l'espace-temps

Les coordonnées cartésiennes ont été imaginées par Descartes au XVII^e siècle et ont été largement utilisées par la suite en mécanique newtonienne pour décrire l'espace physique selon trois dimensions (souvent symbolisées par les lettres x, y, z). La relativité restreinte a constitué une véritable révolution scientifique, et a amené dès les années 1900 des scientifiques comme Henri Poincaré et Hermann Minkowski à concevoir l'espace et le temps comme indissociablement liés, dans ce que l'on appelle l'espace-temps, théorisé par la notion d'espace de Minkowski. Aux trois dimensions d'espace s'ajoute ainsi la quatrième dimension du temps.

Dans cette théorie, Minkowski utilise une représentation simplifiée de l'espace-temps en coordonnées cartésiennes, le diagramme de Minkowski, avec une dimension d'espace et la dimension de temps (symbolisée par ct, où c est la vitesse de la lumière et t le temps), pour rendre compte de phénomènes tels que la dilatation du temps, la contraction des longueurs ou encore la notion de simultanéité, sans utiliser d'équation mathématique.

Introduction historique par Descartes

L'introduction des coordonnées cartésiennes est faite dans le livre premier de la géométrie de René Descartes comme un outil afin de résoudre le problème de Pappus. Il montre en fait dans ce livre, comment résoudre un problème géométrique par un calcul algébrique, participant à la naissance de la géométrie analytique.

« Que le segment de la ligne AB, qui est entre les points A et B, soit nommé x; et que BC soit nommé y ; et que toutes les autres lignes données soient prolongées jusqu’à ce qu’elles coupent ces deux aussi prolongées, s’il est besoin, et si elles ne leur sont point parallèles; comme vous voyez ici qu’elles coupent la ligne AB aux points A, E, G, et BC aux points R, S, T. (...) »

— René Descartes , La géométrie, livre premier .

Annexes

Articles connexes

• Repérage dans le plan et dans l'espace
• Géométrie analytique
• Système de coordonnées
  • Coordonnées cylindriques
  • Coordonnées polaires
  • Coordonnées sphériques
• Diagramme de Minkowski
• Horizontale et verticale

Bibliographie

• [Borceux 2013] (en) Francis Borceux, Geometric trilogy, t. II : An algebraic approach to geometry [« Trilogie de géométrie », t. II : « Une approche algébrique de la géométrie »], Cham, Springer, hors coll., novembre 2013 (réimpr. août 20216), 1^re éd., XVII-430 p., 15,6 × 23,4 cm (ISBN 978-3-319-01732-7 et 978-3-319-34752-3, EAN 9783319017327, OCLC 1129014536, BNF 44674751, DOI 10.1007/978-3-319-01733-4, S2CID 117005292, SUDOC 241124646, présentation en ligne, lire en ligne).
• [Dieudonné 1985] (en) Jean Dieudonné (trad. du français par Judith D. Sally), History of algebraic geometry : an outline of the history and development of algebraic geometry [« Cours de géométrie algébrique traduction, t. I^er »] [« Histoire de la géométrie algébrique : un aperçu de l'histoire et du développement de la géométrie algébrique »], New York, Chapman & Hall, hors coll., mai 1985 (réimpr. décembre 2019), 1^re éd., XII-186 p., 15,8 × 24,7 cm (ISBN 978-0-412-99371-8 et 978-0-367-45170-7, EAN 9780412993718, OCLC 423998623, BNF 37411473, DOI 10.1201/9780203751800, S2CID 197441066, SUDOC 151803226, présentation en ligne, lire en ligne).
• René Descartes, Le Livre Premier de La Géométrie de Descartes, 1637, 18 p. (lire en ligne)