Diagramme de Voronoï

Type	Algorithme, partition, diagramme
Nommé en référence à	Gueorgui Voronoï

En mathématiques, un diagramme de Voronoï est un pavage (découpage) du plan en cellules (régions adjacentes) à partir d'un ensemble discret de points appelés germes. Chaque cellule enferme un seul germe, et forme l'ensemble des points du plan plus proches de ce germe que d'aucun autre. La cellule représente en quelque sorte la « zone d'influence » du germe.

Le diagramme doit son nom au mathématicien russe Gueorgui Voronoï (1868-1908). Le découpage est aussi appelé décomposition de Voronoï, partition de Voronoï ou tessellation de Dirichlet.

De manière plus générale, il représente une décomposition d’un espace métrique en cellules (régions adjacentes), déterminée par les distances à un ensemble discret d’objets de l’espace, en général un ensemble discret de points. Dans le plan les cellules sont appelées polygones de Voronoï ou polygones de Thiessen, et dans l'espace polyèdres de Voronoï.

Histoire

On peut faire remonter l’usage informel des diagrammes de Voronoï jusqu'à Descartes en 1644 dans Principia philosophiae comme illustration de phénomène astronomique^[1]. Dirichlet a utilisé des diagrammes de Voronoï en dimension 2 ou 3 dans son étude des formes quadratiques en 1850 (Dirichlet 1850).

En 1854, le médecin britannique John Snow a utilisé le diagramme de Voronoï pour montrer que la majorité des personnes mortes dans l’épidémie de choléra de Soho se trouvaient dans la cellule de la pompe à eau de Broad Street, donc qu'ils vivaient plus près de cette pompe que de n’importe quelle autre pompe^[2]. Il a ainsi démontré que le foyer de l'infection était cette pompe.

Les diagrammes de Voronoï portent le nom du mathématicien russe Georgy Fedoseevich Voronoï (ou Voronoy) qui a défini et étudié le cas général en dimension $n$ en 1908^[3]^,^[4]. Les diagrammes de Voronoï qui sont utilisés en géophysique et en météorologie pour analyser des données de distributions spatiales (comme les mesures de chutes de pluie) sont appelés polygones de Thiessen du nom du météorologiste américain Alfred H. Thiessen (en).

Définition

On se place dans le plan affine $\mathbb {R} ^{2}$ . Soit $S$ un ensemble fini de $n$ points du plan ; les éléments de $S$ sont appelés centres, sites ou encore germes. On appelle région de Voronoï — ou cellule de Voronoï — associée à un germe $p$ de $S$ , l’ensemble des points qui sont plus proches de $p$ que de tout autre point de $S$ :

\mathrm {Vor_{S}} (p)=\{x\in \mathbb {R} ^{2}\ /\ \forall q\in \mathrm {S} \ \|x-p\|\leq \|x-q\|\}

où $|| x - p ||$ désigne la distance entre n'importe quel point $x$ et le germe $p$ .

Si l'on appelle $H(p, q)$ le demi-plan contenant $p$ délimité par la médiatrice du segment $[pq]$ , on a

\mathrm {H} (p,q)=\{x\in \mathbb {R} ^{2}\ /\ \|x-p\|\leq \|x-q\|\}

.

On peut alors écrire :

\mathrm {Vor_{S}} (p)=\bigcap _{q\in \mathrm {S} \backslash \{p\}}\mathrm {H} (p,q)

.

En dimension 2, il est facile de tracer ces partitions. On se base sur le fait que la frontière entre les cellules de Voronoï de deux germes distincts se situe forcément sur la médiatrice qui sépare ces deux germes. En effet, les points de cette médiatrice sont équidistants des deux germes donc on ne peut pas affirmer qu’ils se situent dans l'une ou l'autre cellule de Voronoi. Pour un ensemble de germes, le diagramme de Voronoï se construit donc en déterminant les médiatrices de chaque couple de germes. Un point d'une médiatrice appartient alors à une frontière de Voronoï s'il est équidistant d'au moins deux germes et qu'il n'existe pas de distance plus faible entre ce point et un autre germe de l'ensemble.

On peut généraliser la notion à un espace euclidien $E$ muni de la distance euclidienne $d$ . Soit $S$ un ensemble fini de $n$ points de E. La définition devient :

\mathrm {Vor_{S}} (p)=\{x\in \mathrm {E} \ /\ \forall q\in \mathrm {S} \ \mathrm {d} (x,p)\leq \mathrm {d} (x,q)\}

Pour deux points $a$ et $b$ de $S$ , l’ensemble $Π(a, b)$ des points équidistants de $a$ et $b$ est un hyperplan affine (un sous-espace affine de co-dimension 1). Cet hyperplan est la frontière entre l’ensemble des points plus proches de $a$ que de $b$ , et l’ensemble des points plus proches de $b$ que de $a$ .

\Pi (p,q)=\{x\in \mathrm {E} \ /\ \mathrm {d} (x,p)=\mathrm {d} (x,q)\}

On note $H(a, b)$ le demi espace délimité par cet hyperplan contenant $a$ , il contient alors tous les points plus proches de $a$ que de $b$ . La région de Voronoï associée à $a$ est alors l’intersection des $H(a, b)$ où $b$ parcourt $S\{a}$ .

\mathrm {H} (p,q)=\{x\in \mathrm {E} \ /\ \mathrm {d} (x,p)\leq \mathrm {d} (x,q)\}

\mathrm {Vor_{S}} (p)=\bigcap _{q\in \mathrm {S} \backslash \{p\}}\mathrm {H} (p,q)

Généralisation du diagramme de Voronoï

Pour résoudre certains problèmes, Shamos^[5] introduit la notion de diagramme de Voronoï d'un ensemble de points $A$ (sous-ensemble de $S$ ), $V(A)$ , défini par :

\mathrm {V} (\mathrm {A} )=\left\{x\in \mathrm {E} /\ \forall p\in \mathrm {A} ,\forall q\in \mathrm {S} \setminus \mathrm {A} ,\mathrm {d} (x,p)<\mathrm {d} (x,q)\right\}

Ainsi, $V(A)$ est l'ensemble des points qui sont plus proches de chaque point de $A$ que de n'importe quel point n'étant pas dans $A$ .

Si l'on appelle $H(i, j)$ le demi-plan délimité par la médiatrice du segment $[ij]$ et contenant $i$ , alors on a :

\mathrm {V} (\mathrm {A} )=\bigcap _{i\in \mathrm {A} ,j\in \mathrm {S} \setminus \mathrm {A} }\mathrm {H} (i,j)

Les régions de Voronoï généralisées sont donc convexes, mais elles peuvent être vides. Shamos définit par la suite les diagrammes de Voronoï d'ordre $k$ (1 ≤ k < card(S)) par la réunion des cellules de Voronoï généralisées formées par tous les sous-ensembles de $k$ points :

\mathrm {V} _{k}(\mathrm {S} )=\bigcup _{\mathrm {A} \subset \mathrm {S} ,\mathrm {card} (\mathrm {A} )=k}\mathrm {V} (\mathrm {A} )

.

Les régions $V(A)$ forment une partition de $V k (S)$ .

Il définit également le « diagramme de Voronoï des points les plus éloignés » (farthest-point Voronoi diagram). Ce diagramme est construit en inversant le sens de l'inégalité

{\overline {\mathrm {Vor} }}_{\mathrm {S} }(p)=\left\{x\in \mathrm {E} \ /\ \forall q\in \mathrm {S} \ \mathrm {d} (x,p)\geq \mathrm {d} (x,q)\right\}

Le point $p$ ne se trouve évidemment pas dans la cellule $Vor S (p)$ , mais à l'opposé par rapport au « centre » de l'ensemble : le point $p$ est le point de $S$ le plus éloigné de $Vor S (p)$ .

Le diagramme des points les plus éloignés est entièrement déterminé par l'enveloppe convexe de $S$ . Il ne contient pas de cellule fermée.

Ainsi, l'ensemble des points les plus éloignés d'un point $p$ est l'ensemble des points qui sont plus proches des autres points de $S$ :

{\overline {\mathrm {Vor} }}_{\mathrm {S} }(p)=\bigcup _{q\in \complement _{\mathrm {S} }(\{p\})}\mathrm {Vor_{S}} (q)

donc le diagramme des points les plus éloignés est identique à $V n - 1 (S), n = card(S)$ .

Propriétés

Les régions de Voronoï sont des polytopes convexes en tant qu’intersection de demi espaces^[a]. L’ensemble de tels polygones partitionne E, et est la partition de Voronoï correspondant à l’ensemble $S$ .

Théorème — Soit $v$ un point du plan. C'est un sommet d'un polygone de Voronoï si et seulement si c'est le centre d'un cercle passant par trois germes, et ne contenant aucun autre germe dans sa surface.

Démonstration

Le point $v$ se trouve à l'intersection de trois cellules $Vor S (p)$ , $Vor S (q)$ et $Vor S (r)$ , il est donc à égale distance de $p$ , $q$ , $r$ , donc $v$ est le centre du cercle circonscrit à $pqr$ . Si un autre germe se trouvait dans le disque, alors $v$ serait plus proche de ce point que de $p$ , $q$ et $r$ , il ne se trouverait donc dans aucune des trois cellules.

Une autre propriété est que les deux points les plus rapprochés sont dans des cellules adjacentes.

Relation avec la triangulation de Delaunay

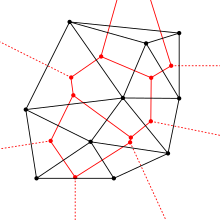
Le diagramme de Voronoï d’un ensemble discret $S$ de points est le graphe dual de la triangulation de Delaunay associée à $S$ .

Passage du diagramme de Voronoï à la triangulation de Delaunay

Chaque germe du diagramme de Voronoï constitue un sommet dans la triangulation de Delaunay. Ces sommets sont reliés entre eux par une arête si et seulement si les cellules sont adjacentes.

\mathrm {DEL} (\mathrm {S} )=\{(p,q)\in \mathrm {S} ^{2}\ /\ \mathrm {Vor_{S}} (p)\cap \mathrm {Vor_{S}} (q)\neq \varnothing \}

Passage de la triangulation de Delaunay au diagramme de Voronoï

Les sommets du diagramme de Voronoï sont les centres des cercles circonscrits des triangles de la triangulation de Delaunay. Les arêtes du diagramme de Voronoï sont sur les médiatrices des arêtes de la triangulation de Delaunay.

Représentation du diagramme

Graphiquement, on représente en général les parois des cellules, c'est-à-dire les points qui sont à égale distance d'au moins deux centres, et les centres associés aux cellules. On représente parfois la cellule par un aplat de couleur, avec ou sans paroi, avec une couleur différente entre chaque cellule (voir Théorème des quatre couleurs).

D'un point de vue analytique, une cellule étant une intersection de demi-plans, elle peut être représentée comme le système d'équation de ces demi-plans (voir Géométrie analytique > Demi-plan) :

\left\{{\begin{matrix}a_{1}x+b_{1}y\geqslant c_{1}\\a_{2}x+b_{2}y\geqslant c_{2}\\\cdots \end{matrix}}\right.

Pour représenter informatiquement un diagramme de Voronoï, John Burkardt^[6] a proposé d'utiliser un fichier avec quatre types d'enregistrement :

s x y : point de l'ensemble $S$ , de coordonnées $(x, y)$ ;
v x y : sommet (vertex) d'un polygone de Voronoï, de coordonnées $(x, y)$ ;
l a b c : droite (portant une arête d'un polygone), d'équation $ax + by = c$ ;
e l v1 v2 : arête d'un polygone, décrit par l'indice $l$ de sa droite porteur et les indices $v 1$ et $v 2$ des sommets qui sont ses extrémités ; si un indice est égal à –1, cela signifie que le sommet est « à l'infini » (demi-droite, ou droite si les deux sommets sont à –1).

Algorithmes

Algorithme de Green et Sibson

L'algorithme de Green et Sibson est un algorithme incrémental pour calculer un diagramme de Voronoï^[7]. Il maintient un diagramme de Voronoï en ajoutant les points un à un. Sa complexité est $O(n^{2})$ .

Algorithme de Shamos et Hoey

Article détaillé : Algorithme de Shamos et Hoey.

Shamos et Hoey ont montré en 1975^[5] qu'il est possible de calculer le diagramme de Voronoï d'un ensemble de $n$ points du plan dans le temps $O(n log n)$ . Ils utilisent pour cela un raisonnement par récurrence : supposons que l'on puisse séparer l'ensemble $S$ en deux sous-ensembles de même cardinal $n /2$ , séparés par une droite verticale : l'ensemble $G$ des points à gauche et l'ensemble $D$ des points à droite. Les diagrammes respectifs de ces sous-ensembles, V(G) et V(D), sont connus, et on peut les fusionner. On a ainsi un algorithme de type diviser pour régner, dont la complexité est $O(n log n)$ .

Algorithme de Fortune

L'algorithme de Fortune (1987, Laboratoires Bell AT&T)^[8] a été démontré comme asymptotiquement optimal. Il est en $O(n log n)$ en temps et en $O(n)$ en espace mémoire.

L'idée générale consiste à balayer le plan de gauche à droite avec une ligne verticale (c'est un algorithme de sweep line) ; on construit le diagramme de Voronoï progressivement. Le problème est que le diagramme déjà construit, à gauche de la ligne, dépend de points situés à droite de cette ligne, et donc non encore pris en compte. Fortune résout ce problème en considérant un front parabolique légèrement « en retard » par rapport à la droite de balayage, tel que le diagramme situé à gauche de ce front est le diagramme final.

Algorithme de Bowyer-Watson

L'algorithme de Bowyer-Watson calcule une triangulation de Delaunay, on peut ensuite passer au dual pour obtenir le diagramme de Voronoi.

Applications

Les diagrammes de Voronoï sont utilisés, ou réinventés sous de nombreux noms, dans différents domaines. Ils interviennent souvent lorsque l'on cherche à partitionner l'espace en zones d'influence. Quelques exemples :

Astronomie

partition des structures spatiales des populations d'étoiles ;

Biologie et médecine

diagnostic de cellules cancéreuses ;

Économie et administration

pour l'organisation territoriale, si les points correspondent à des ressources, les cellules de Voronoï correspondent aux territoires que desservent ces ressources de manière optimale, en considérant que l'effort d'accès est proportionnel à la distance à vol d'oiseau et que la densité de population est uniforme ; par exemple, établissement de la carte scolaire ;
géomarketing ;

Géographie

reconstruction de données géographiques optimales, pour un simulateur de vol par exemple ;
simulation de paysages, notamment agricoles (les cellules de Voronoï pouvant être assimilées à des parcelles de cultures) ;
génération de cartes, principalement utilisé pour les jeux vidéos ou dans un usage créatif^[9] ;

Image

effet de mosaïque dans un logiciel de retouche d'image ;

Mathématiques

construction d'un dôme géodésique dual ;
résolution d'un certain nombre de problèmes de géométrie, avec souvent des applications d'optimisation spatiale (logistique, aménagement du territoire, emplacement d'une installation)^[5] :
- recherche des plus proches voisins,
- problème du plus grand cercle vide,
- problème du voyageur de commerce,
- détermination de l'enveloppe convexe,
- problème du cercle minimum,
- caractérisation de la desserte d'aires de livraison en ville^[10] ;

Physique et chimie

modélisation de microstructures, telles que celles de certains aciers ;
simulation de la circulation des fluides dans les milieux poreux, en particulier avec la méthode des éléments naturels ;
en cristallographie, détermination de la maille de Wigner-Seitz et de la zone de Brillouin ;
en thermodynamique chimique, modélisation des fonctions d'état^[11] ;

Technologies

calculs de trajectoire en robotique mobile ;
détection dans les systèmes de communications sans fil (en particulier, notion de téléphonie cellulaire).

Football

déterminer la zone de contrôle d’un joueur donné à un instant quelconque du match

Notes et références

Notes

↑ Voir Ensemble convexe > Intersections de convexes

Références

↑ Principia philosophiae 1644, édition latine AT VIII-1 ; traduction française par Paul Picot, revue par Descartes, Les Principes de la philosophie, 1647 avec une Lettre-Préface AT IX-2
↑ (en) Steven Johnson, The Ghost Map : The Story of London's Most Terrifying Epidemic – and How it Changed Science, Cities and the Modern World, New York, Riverhead Books, 2006, 299 p. (ISBN 1-59448-925-4), p. 195–196
↑ Georges Voronoï, « Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Premier mémoire. Sur quelques propriétés des formes quadratiques positives parfaites. », Journal für die Reine und Angewandte Mathematik, vol. 1908, n^o 133,‎ 1908, p. 97–178 (lire en ligne)
↑ Georges Voronoï, « Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Premier mémoire. Sur quelques propriétés des formes quadratiques positives parfaites. », Journal für die Reine und Angewandte Mathematik, vol. 1908, n^o 134,‎ 1908, p. 198–287 (lire en ligne)
↑ ^{a b et c} (en) Michael Ian Shamos, Computational Geometry : thèse de doctorat, université Yale, 1975
(en) Michael Ian Shamos et Dan Hoey, « Closest-point problems », dans Proceeding of 16th Annual IEEE Symposium on Foundations of Computer Science, Los Angeles, IEEE Computer Society Press, 1975 (lire en ligne), p. 151-162
↑ Voronoi and Delaunay Calculations, Université d'État de Floride
↑ Franck Hétroy, « Un peu de géométrie algorithmique, 4.2 Voronoı̈ : construction incrémentale », sur ENSIMAG.
↑ (en) Steven Fortune, « A Sweepline Algorithm for Voronoi Diagrams », Algorithmica, Springer-Verlag, vol. 1,‎ 1987, p. 153-174
↑ (en) Amit J. Patel, « Polygonal Map Generation for Games », Red Blob Games,‎ 4 septembre 2010 (lire en ligne )
↑ (en) Lopez, C., Zhao, C.-L., Magniol, S., Chiabaut, N. et Leclercq, L., « Microscopic Simulation of Cruising for Parking of Trucks as a Measure to Manage Freight Loading Zone », Sustainability, 11 (5), 1276,‎ 28 février 2019 (lire en ligne)
↑ (en) Yongjian Yang, Hirofumi Tokunaga, Madoka Ono, Kazutaka Hayashi et John C. Mauro, « Understanding the molar volume of alkali-alkaline earth-silicate glasses via Voronoi polyhedra analysis », Scripta Materialia (en), vol. 166,‎ juin 2019, p. 1-5 (DOI 10.1016/j.scriptamat.2019.02.041).

Voir aussi

Bibliographie

[Dirichlet 1850] (de) Johann Peter Gustav Dirichlet, « Über die Reduction der positiven quadratischen Formen mit drei unbestimmten ganzen Zahlen », Journal für die reine und angewandte Mathematik,‎ 1850
[Aurenhammer 1991] (en) Franz Aurenhammer, « Voronoi diagrams : a survey of a fundamental geometric data structure », ACM Computing Surveys, vol. 23, n^o 3,‎ septembre 1991, p. 345–405 (lire en ligne)

Articles connexes

Liens externes

Stéphane Bessy, « Algorithmique géométrique : algorithmes du cours », sur LIRMM (consulté le 30 janvier 2017)

[6] Voir Ensemble convexe > Intersections de convexes

[1] Principia philosophiae 1644, édition latine AT VIII-1 ; traduction française par Paul Picot, revue par Descartes, Les Principes de la philosophie, 1647 avec une Lettre-Préface AT IX-2

[2] (en) Steven Johnson, The Ghost Map : The Story of London's Most Terrifying Epidemic – and How it Changed Science, Cities and the Modern World, New York, Riverhead Books, 2006, 299 p. (ISBN 1-59448-925-4), p. 195–196

[3] Georges Voronoï, « Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Premier mémoire. Sur quelques propriétés des formes quadratiques positives parfaites. », Journal für die Reine und Angewandte Mathematik, vol. 1908, n^o 133,‎ 1908, p. 97–178 (lire en ligne)

[4] Georges Voronoï, « Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Premier mémoire. Sur quelques propriétés des formes quadratiques positives parfaites. », Journal für die Reine und Angewandte Mathematik, vol. 1908, n^o 134,‎ 1908, p. 198–287 (lire en ligne)

[shamos-5] {a b et c} (en) Michael Ian Shamos, Computational Geometry : thèse de doctorat, université Yale, 1975
(en) Michael Ian Shamos et Dan Hoey, « Closest-point problems », dans Proceeding of 16th Annual IEEE Symposium on Foundations of Computer Science, Los Angeles, IEEE Computer Society Press, 1975 (lire en ligne), p. 151-162

[7] Voronoi and Delaunay Calculations, Université d'État de Floride

[Hétroy-8] Franck Hétroy, « Un peu de géométrie algorithmique, 4.2 Voronoı̈ : construction incrémentale », sur ENSIMAG.

[9] (en) Steven Fortune, « A Sweepline Algorithm for Voronoi Diagrams », Algorithmica, Springer-Verlag, vol. 1,‎ 1987, p. 153-174

[10] (en) Amit J. Patel, « Polygonal Map Generation for Games », Red Blob Games,‎ 4 septembre 2010 (lire en ligne )

[11] (en) Lopez, C., Zhao, C.-L., Magniol, S., Chiabaut, N. et Leclercq, L., « Microscopic Simulation of Cruising for Parking of Trucks as a Measure to Manage Freight Loading Zone », Sustainability, 11 (5), 1276,‎ 28 février 2019 (lire en ligne)

[12] (en) Yongjian Yang, Hirofumi Tokunaga, Madoka Ono, Kazutaka Hayashi et John C. Mauro, « Understanding the molar volume of alkali-alkaline earth-silicate glasses via Voronoi polyhedra analysis », Scripta Materialia (en), vol. 166,‎ juin 2019, p. 1-5 (DOI 10.1016/j.scriptamat.2019.02.041).

[1]

[2]

[3]

[4]

[5]

[a]

[6]

[7]

[8]

[9]

[10]

[11]