Heure archaïque

Indicateurs solaires antiques égyptiens.

Les heures archaïques sont des essais de division du jour dans les civilisations de la Haute-Antiquité.

Dérivée du grec ancien ὥρα puis du latin hora, l'heure, dont le sens était plus large qu'aujourd'hui, est un terme dont les origines ne remontent qu'aux environs du V^e siècle av. J.-C. Avant cette époque, l'heure n'existait donc pas en tant que telle ; dans certaines civilisations anciennes, les essais de division du jour, remontant jusqu'avant le deuxième millénaire av. J.-C., seront néanmoins désignés par le terme générique d'« heure », plus précisément qualifiées d'« heures archaïques » (ou primitives).

Ces heures archaïques seront suivies dans l'époque historique de l'Antiquité par de véritables heures : les heures temporaires et les heures équinoxiales qui perdureront au-delà de cette époque.

En Mésopotamie

Chez les Assyriens, à la fin du troisième millénaire avant notre ère, l'arithmétique et l'astronomie se développent. On compte en base 60, l'année comporte douze mois de trente jours avec un mois intercalaire qui est introduit quand la différence entre l'année civile et l'année physique est trop importante. Le nycthémère comporte six veilles de jour (donc de durée variable, comme la longueur du jour) et six veilles de nuit - ou trois suivant les auteurs -, les kaspu, dont on ne sait pas grand-chose. Ces kaspu ou bēru ou danna valaient donc en moyenne deux de nos heures.

En Égypte

Les Égyptiens ont été les premiers à mettre en place un calendrier solaire de 365 jours et la première mention des heures se situe aux environs de -2350.

L'année antique égyptienne comprend trois saisons de quatre mois de trente jours, plus cinq jours épagomènes, soit 365 jours. Chaque mois est fait de trente jours regroupés en trois décades. C'est dans ce contexte, dans le milieu mythologique religieux des prêtres astronomes que vont naître les heures.

Scarabée et disque solaire entourés de babouins hamadryas représentation de Thot.

Heures décanales

Sarcophage de Idy, chaque case comporte le nom d'une étoile ;
les dieux représentés sont de g. à d. : La Grande Ourse, la Voie Lactée ?, Orion (3 rois) ; Sothis ou Sirius.

Tableau de distribution des étoiles décanales.

Sur le couvercle de sarcophages de hauts dignitaires égyptiens datant d'environ -2150, est peinte une grille calendaire avec, pour chaque décade, une division en douze parties.

Cette représentation correspond au voyage symbolique de l'âme du défunt dans l'au-delà, à travers la voute céleste constellée d'étoiles assimilées à des dieux ; elle peut être expliquée à partir d'un tableau, condensé d'une horloge stellaire égyptienne.

Ce tableau correspond à une des saisons de l'année censée être représentée.

Verticalement, les colonnes I, II, III, IV représentent les trois mois de la saison. Chaque mois comprend trois colonnes décadaires.

Sur chaque ligne, dans une case se trouve une lettre A, B, C… qui correspond à une étoile représentative de la décade considérée.

Chaque ligne horizontale matérialise des intervalles de temps Δt. Ces Δt ou heures sont au nombre de douze, elles représentent les moments où l'âme du défunt est censée croiser une étoile. Ce sont donc des heures de nuit qui sont représentées. Sur le sarcophage, à chaque case du tableau correspond le nom d'une étoile.

Le trait horizontal blanc situé entre la sixième et la septième heure correspond au milieu de la nuit, instant d'offrandes.

Pour la première décade du premier mois I, l'étoile A correspond au début de la nuit et l'étoile L à la fin de la nuit. Le premier jour du décan est marqué par le lever de l'étoile L avant l'apparition du Soleil à l'est, c'est le lever héliaque de l'étoile. Dix jours plus tard, l'étoile L qui se lève de plus en plus tôt par rapport au Soleil s'enfonce dans la nuit et elle va céder la place à l'étoile M qui marquera par son lever héliaque le deuxième décan du mois. Le développement complet de la description et du fonctionnement de cette horloge décanale se trouve sur la page Horloge stellaire égyptienne.

Instant du lever héliaque de Sirius, photo montage.

Ainsi donc, la nuit est divisée théoriquement en douze heures stellaires, quelle que soit la longueur de la nuit. Ces heures sont donc de durée variable en fonction des saisons, mais elles le sont aussi par l'instant du lever héliaque de chaque étoile : l'instant de ce lever, le premier jour d'une décade, peut être situé, entre une demi-heure et une heure avant le lever du Soleil, en fonction de la magnitude de l'étoile considérée, puis ce lever va « avancer » de quatre minutes chaque nuit tout au long de la décade soit quarante minutes au total sur dix jours. L'origine temps de la nuit n'est pas connu ; on peut supposer que c'est l'observation du lever héliaque qui peut être pris en considération, à moins qu'il s'agisse du coucher héliaque ou du milieu de la nuit ?

Schéma de mise en place d'heures décanales.

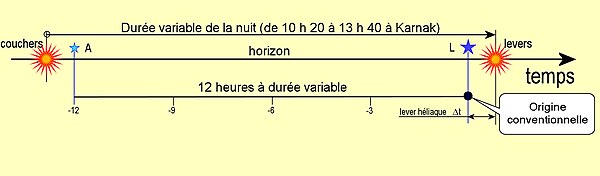
Comme précisé plus haut, cette division de la nuit est théorique ou plutôt virtuelle. Elle ne concerne pas les vivants ! Seuls le lever ou le coucher héliaques, qui sont des évènements physiques, et éventuellement le repérage du milieu de la nuit où des offrandes sont offertes aux dieux, sont du ressort de l'humain.

Heures de gnomon

Dans le courant du deuxième millénaire avant notre ère, toujours dans le milieu des prêtres et des pharaons, il y aura diverses tentatives pour passer des heures virtuelles de la nuit à des heures physiques matérialisées par des instruments analogiques tels les indicateurs solaires, les « clepsydres » et les horloges stellaires ramessides.

Dans le domaine des instruments solaires, il semble qu'au Moyen Empire, soit avant -1786, il ait existé des tables d'ombre. Les tables d'ombre donnent, en principe, la longueur de l'ombre d'un gnomon en fonction de la date de l'année et de l'heure du jour ; malheureusement, l'information est donnée sans plus de précisions.

Règle en L d'Amenhotep III, Musée du Louvre, Paris.

Entre les années -1500 et -1000, apparaissent dans le mobilier funéraire de certaines tombes de pharaons des règles en L, sortes d'indicateurs solaires. Un talon fait office de gnomon et des marques sur la partie tenue horizontale ont vraisemblablement pour fonction d'indiquer des hauteurs du Soleil ou des « heures » quand l'instrument est aligné avec le Soleil.

Sur ces règles en L, le nombre de marques est différent suivant le mobilier découvert ; ces marques sont au nombre de quatre ou cinq (vers - 1279, sous Séthi I^er), cinq (vers -1457, sous Amenhotep III et vers -1425 sous Thoutmôsis III) ou six (vers -1000). Diverses hypothèses peuvent être envisagées sur leur fonction :

Inscription du cénotaphe de Séthi I^er à Abydos.

• s'il s'agit d'indications sur la hauteur méridienne du Soleil au cours de l'année, la première et la dernière des marques doivent indiquer les moments des solstices, l'instrument étant orienté vers le Sud comme une méridienne - les marques intermédiaires étant supposées réparties arbitrairement dans l'année. En fonction de la latitude du lieu où ces règles ont été trouvées, il est possible de valider ou non cette hypothèse. Sur la figure donnée ci-après, pour la représentation de la règle d'Amenhotep supposée être utilisée vers Louxor-Karnak, on voit que cette hypothèse est absurde ; on voit d'ailleurs, que la règle n'est pas utilisable pour une grande période de l'hiver, l'ombre de midi tombant dans ce cas dans l'intervalle 4-5.

Midi au Soleil, aux solstices, à Louxor.

• s'il s'agit d'indications « horaires », pour une même latitude, la hauteur du Soleil variant en fonction des saisons pour une même heure, cette hypothèse doit être, elle aussi, rejetée ;

Heures solaires égales d'été et d'hiver à Louxor.

• il peut peut-être s'agir de la transposition d'une table d'ombre simple, pour une saison donnée comme indiqué ci-dessous, la table d'ombre correspondant aux deux dernières colonnes du tableau. Chaque intervalle correspondrait alors à une « heure de gnomon ». Cette hypothèse est-elle plausible ?

Règle en L d'Amenhotep III, transposition d'une table d'ombre ?

Marque	Long.	Long / h gnomon		L f(h gnomon)	Long. ombre
1	105	5,25		5	100
2	70	3,5		3,5 ou 7/2	70
3	43	2,15		2	40
4	25	1,25		1	20
5	10	0,5		0,5 ou 1/2	10
6	0	-		-	-

• pour finir, il peut s'agir tout simplement de marquer des instants, instants de dévotions par exemple, ou de définir des intervalles de temps visuels divisant les deux demi-journées grossièrement en quatre, cinq ou six parties.

Ces deux dernières hypothèses (instants ou divisions) sont les plus vraisemblables. Pour finir, après comparaison avec de véritables heures temporaires, on s'aperçoit qu'il n'existe guère de lien avec la réalité physique des heures. Ces marques sont donc considérées aujourd'hui, comme indéterminées et tracées très probablement de façon empirique.

• Comparaison aux heures temporaires
• 
  Cadran d'heures temporaires.
• 
  Application à la règle en L d'Amenhotep III.

De ces règles en L, on ne peut déduire que :

• le demi-jour était divisé empiriquement en n parties, de quatre à six (probable) en fonction du mobilier trouvé ;
• l'origine du jour était possiblement le lever du Soleil à l'horizon impossible à marquer sur une règle horizontale ; il pourrait s'agir plus vraisemblablement de la fin de la nuit marquée par le lever héliaque des étoiles de référence, ceci pour faire le lien jour-nuit dans un nyctémère.

Schéma de mise en place des heures de gnomon.

Plus tard, des instruments plus élaborés, telle la règle pentée étudiée par Ludwig Borchardt et datant d'environ -320 ont été considérés comme horloges solaires : en -320, les premiers cadrans solaires grecs existent et les inscriptions sur l'horloge de Borchardt étant en grec, ce ne serait alors qu'une adaptation à un instrument égyptien d'informations fournies par les cadrans grecs. Une analyse gnomonique du matériel serait néanmoins souhaitable pour infirmer ou confirmer l'hypothèse de Borchardt.

Règle pentée (-320), d'après Borchardt.

Heures de clepsydre

Extérieur d'une clepsydre, telle celle de Karnak.

Les clepsydres égyptiennes, qui sont en fait des horloges hydrauliques primitives, font leur apparition dans la vallée du Nil vers -1500 et la plus ancienne connue, la clepsydre de Karnak est datée de -1350. Elles succèdent aux horloges stellaires du millénaire précédent, et en sont un peu leur transposition.

La clepsydre de Karnak est bien documentée ; elle indique des heures de nuit.

1. l'intérieur de l'instrument, de forme tronconique, permet un écoulement régulier et quasiment constant de l'eau qui s'y trouve ;
2. son pourtour est gravé des douze mois égyptiens ; en correspondance, douze colonnes de marques horaires permettent de diviser la nuit égyptienne en douze heures, quel que soit le mois considéré ;
3. la nuit la plus courte mesure douze doigts et la plus longue quatorze.

Développement de l'intérieur de la clepsydre de Karnak.

Analysons ces informations.

Profil théorique et réel de la forme intérieure d'une clepsydre, pour un débit constant.

1. cette forme tronconique a probablement été déterminée par tâtonnement en se référant au temps d'écoulement d'une clepsydre élémentaire servant d'unité de temps ;
2. pour chaque mois, les heures sont identiques de la première à la troisième décade, convention simplificatrice ;
3. concernant la durée de la nuit :
   1. la plus courte fait douze doigts, la plus longue quatorze : cette durée mensuelle, comme précédemment peut être mesurée avec une clepsydre élémentaire servant d'unité de temps ;
   2. Mais, qu'appelle-t-on nuit égyptienne ? Est-ce le temps entre coucher et lever du Soleil ou temps entre coucher et lever héliaques d'étoiles décanales ? Si on considère la latitude de Karnak, lieu supposé d'utilisation de la clepsydre, la nuit entre le coucher et le lever du Soleil, aux alentours de -1500, varie de 10,36 h en été à 13,64 h en hiver, soit un rapport grossier de 10,5 à 13,75 ou de 10,7 / 14, ce qui ne correspond pas au rapport 12 / 14 servant à la division des heures dans la clepsydre. Si on se base sur le coucher et le lever héliaque d'étoiles décanales, avec un décalage moyen de ± 3/4 d'heure par rapport au Soleil, ce rapport descend à 10,2 / 14, ce qui est encore plus éloigné de la référence 12 / 14.

On déduira de cette analyse que :

• l'origine de la nuit, instant potentiel de mise en œuvre de la clepsydre, est équivoque : Est-ce le coucher du Soleil ou le coucher héliaque d'une étoile de référence ;
• les heures, dont la longueur varie conventionnellement chaque mois, sont grossièrement évaluées.

Schéma de visualisation des heures de clepsydre.

Les horloges stellaires ramessides constituent une application intéressante de la clepsydre qui était certainement difficile à exploiter la nuit. Ces horloges, s'appuyant sur des tables de lecture trouvées dans des tombes de pharaons (ca. -1137 à -1108), permettaient d'appréhender l'heure la nuit. Sommairement, la nuit était divisée en douze heures de clepsydre, et, à chaque heure de la nuit correspondait une étoile passant au méridien. C'est ce passage au méridien qui donnait l'heure de la nuit, par lecture de tables dédiées.

Fonctionnement d'une horloge ramesside.

L'indication des heures de la nuit, bien qu'approximative, devait suffire aux prêtres égyptiens, et globalement, ces heures de clepsydre sont, dans l'antique Égypte, l'approche la plus fine qui soit des heures dites historiques qui vont bientôt leur succéder.

Annexes

Bibliographie

 : document utilisé comme source pour la rédaction de cet article.

• (de) Ludwig Borchardt, Die altägyptische Zeitmessung, Leipzig et Berlin, 1920.
• Jérôme Bonnin, La mesure du temps dans l'Antiquité, Paris, Les Belles Lettres, 2015, 444 p. (ISBN 978-2-251-44509-0).
• Denis Savoie, La gnomonique, Paris, Les Belles Lettres, 2007, 521 p. (ISBN 978-2-251-42030-1).
• Raymond D'Hollander, Sciences géographiques dans l'antiquité : connaissance du monde, conception de l'univers, Paris, Aft et Ign, 2002, 465 p. (ISBN 2-901264-53-0).

Articles connexes

• Le jour et ses subdivisions en Mésopotamie

Liens externes

• Revue Archeologia : CS Rome