Liste des groupes d'espace
Il existe 230 types de groupes d'espace en trois dimensions, dénommés par un index numérique et un symbole de Hermann-Mauguin, appelé aussi symbole international (abrégé, complet ou étendu). Le symbole est parfois donné avec des espaces pour une meilleure lisibilité. À chaque type de groupe ponctuel de symétrie cristallographique correspond un ou plusieurs types de groupe d'espace.
Symboles
[modifier | modifier le code]Dans la notation de Hermann-Mauguin, les groupes d'espace sont nommés par un symbole qui contient une lettre majuscule décrivant le type de réseau et, pour chaque direction de symétrie du réseau, les éléments de symétrie. Lorsque plusieurs éléments de symétrie coexistent le long d’une direction de symétrie, dans le symbole du groupe d’espace on en choisit un selon la règle de priorité suivante :
- les axes de rotation sont prioritaires par rapport aux axes hélicoïdaux ayant la même composante de rotations ;
- les miroirs sont choisis selon la priorité suivante : m>e>a,b,c>n>d.
Des exceptions existent toutefois, notamment dans le cas des groupes I222 vs. I212121 et de leur supergroupes cubiques I23 vs. I213. Dans ces groupes, un axe de rotation et un axe hélicoïdal coexistent le long des trois directions [100], [010], [001]. Dans I222 et I23 les axes de rotation se croisent en un point, alors que cela n’est pas vrai pour I212121 et I213. Pour différencier ces deux paires de groupes, la convention ci-dessous n’est pas suivie pour I212121 et I213.
Le plan de réflexion m est le seul que l'on peut trouver dans un groupe ponctuel. Dans un groupe d'espace, en revanche, on trouve aussi des miroirs translatoires ou plans de glissement, désignés par a, b ou c lorsque la direction de glissement est parallèle à un vecteur de base. Selon le choix de la maille, on trouve aussi le glissement n qui est un glissement le long de la moitié d'une diagonale d'une face de la maille, et le glissement d qui est le long d'un quart d'une diagonale d'une face ou dans l'espace de la maille unitaire. Le glissement d est souvent appelé le plan de glissement du diamant car il apparaît dans la structure de diamant.
- , ou , plan de glissement de cette face le long de la moitié d'un vecteur de la maille unitaire perpendiculaire à la face.
- , plan de glissement le long de la moitié de la diagonale d'une face.
- , plan de glissement le long d'un quart de la diagonale d'une face.
- , deux translations selon le même plan de glissement et une autre le long de la somme de deux vecteurs de la moitié de deux paramètres de la maille.
Un axe de rotation peut être remplacé par un axe hélicoïdal et est noté par le nombre n, qui correspond à l'angle de rotation de cet axe : . La longueur de la translation est alors ajoutée sous la forme d'un indice indiquant quelle est sa mesure le long de l'axe, c'est-à-dire la fraction du vecteur du paramètre de la maille parallèle. Par exemple, 21 est une rotation à 180 °, suivie d'une translation de ½ selon le vecteur de maille parallèle à l'axe de rotation. 31 correspond à une rotation de 120° suivie d'une translation de la moitié du vecteur de la maille parallèle à l'axe de rotation.
Les axes hélicoïdaux possibles sont: 21, 31, 32, 41, 42, 43, 61, 62, 63, 64 et 65.
Un type de groupe d'espace peut avoir jusqu'à trois symboles de Hermann-Mauguin :
- le symbole court, qui ne montre le long de chaque direction de symétrie que le nombre indispensable d'éléments de symétrie pour générer et représenter le groupe ;
- le symbole complet, qui montre chaque type d'élément de symétrie le long de chaque direction de symétrie ;
- le symbole étendu, bâtit sur le symbole court mais qui montre les éléments parallèles entre eux.
Par exemple, le groupe nº 72 est représenté par le symbole court Ibam, le symbole complet I2/b2/a2/m et le symbole étendu ci-dessous.
| I | b | a | m |
| c | c | n |
Dans la notation Schoenflies, le symbole d'un groupe d'espace est représenté par le symbole du groupe ponctuel correspondant avec un exposant supplémentaire. Cet exposant ne donne aucune information supplémentaire sur les éléments de symétrie du groupe d'espace. Il est lié à l'ordre dans lequel Shoenflies a décrit ces groupes d'espace.
Dans la notation Fedorov, le type de groupe d'espace est noté s (symmorphique), h (hémisymmorphique) ou a (asymmorphique). Cette lettre est suivie d'un nombre lié à l'ordre dans lequel Fedorov a décrit ces groupes d'espace. Les groupes d'espace qui correspondent au même groupe ponctuel peuvent être classés en symmorphiques (73), hémisymmorphiques (54) et asymmorphiques (103) :
- dans les groupes symmorphiquse le groupe de symétrie du site de la position de Wyckoff de moindre multiplicité est isomorphe du groupe ponctuel; les symboles de ces groupes ne présentent, outre que la lettre indiquant le type de maille conventionnelle, que des éléments de symétrie sans translation, car les opérations correspondantes peuvent être choisies, avec les translations, comme générateurs du groupe d'espace ;
- dans les groupes hémisymmorphiques, le groupe de symétrie du site de la position de Wyckoff de moindre multiplicité est un sous-groupe d'indice 2 du groupe correspondant dans le groupe symmorphique et ne contient que des opérations de première espèce ;
- tous les autres groupes d'espace sont asymmorphiques.
Par exemple, pour le groupe ponctuel de symétrie 4/mmm :
- les groupes d'espace symmorphiques sont P4/mmm (, 36s) et I4/mmm (, 37s) ;
- les groupes d'espace hémisymmorphiques doivent contenir une combinaison axiale 422, ce sont P4/mcc (, 35h), P4/nbm (, 36h), P4/nnc (, 37h) et I4/mcm (, 38h).
Liste des groupes tricliniques
[modifier | modifier le code]
|
| Numéro | Groupe ponctuel | Symbole abrégé | Symbole complet | Schoenflies | Fedorov | Shubnikov |
|---|---|---|---|---|---|---|
| 1 | 1 | P1 | P 1 | 1s | ||
| 2 | 1 | P1[1] | P 1 | 2s |
Liste des groupes monocliniques
[modifier | modifier le code]| Simple (mP) |
Centré faces C (mC) |
|---|---|
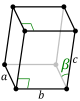
|

|
| Numéro | Groupe ponctuel | Nom abrégé | Noms complets | Schoenflies | Fedorov | Shubnikov | |
|---|---|---|---|---|---|---|---|
| 3 | 2 | P2 | P 1 2 1 | P 1 1 2 | 3s | ||
| 4 | 2 | P21 | P 1 21 1 | P 1 1 21 | 1a | ||
| 5 | 2 | C2 | C 1 2 1 | B 1 1 2 | 4s | ||
| 6 | m | Pm | P 1 m 1 | P 1 1 m | 5s | ||
| 7 | m | Pc | P 1 c 1 | P 1 1 b | 1h | ||
| 8 | m | Cm | C 1 m 1 | B 1 1 m | 6s | ||
| 9 | m | Cc | C 1 c 1 | B 1 1 b | 2h | ||
| 10 | 2/m | P2/m | P 1 2/m 1 | P 1 1 2/m | 7s | ||
| 11 | 2/m | P21/m | P 1 21/m 1 | P 1 1 21/m | 2a | ||
| 12 | 2/m | C2/m | C 1 2/m 1 | B 1 1 2/m | 8s | ||
| 13 | 2/m | P2/c | P 1 2/c 1 | P 1 1 2/b | 3h | ||
| 14 | 2/m | P21/c[2] | P 1 21/c 1 | P 1 1 21/b | 3a | ||
| 15 | 2/m | C2/c[3] | C 1 2/c 1 | B 1 1 2/b | 4h | ||
Liste des groupes orthorhombiques
[modifier | modifier le code]| Primitif (oP) |
Centré (oI) |
centré faces C (oC) |
Faces centrées (oF) |
|---|---|---|---|

|

|

|

|
| Numéro | Groupe ponctuel | Symbole abrégé | Symbole complet | Schoenflies | Fedorov | Shubnikov |
|---|---|---|---|---|---|---|
| 16 | 222 | P222 | P 2 2 2 | 9s | ||
| 17 | 222 | P2221 | P 2 2 21 | 4a | ||
| 18 | 222 | P21212 | P 21 21 2 | 7a | | |
| 19 | 222 | P212121 | P 21 21 21 | 8a | | |
| 20 | 222 | C2221 | C 2 2 21 | 5a | ||
| 21 | 222 | C222 | C 2 2 2 | 10s | ||
| 22 | 222 | F222 | F 2 2 2 | 12s | ||
| 23 | 222 | I222 | I 2 2 2 | 11s | ||
| 24 | 222 | I212121 | I 21 21 21 | 6a | ||
| 25 | mm2 | Pmm2 | P m m 2 | 13s | ||
| 26 | mm2 | Pmc21 | P m c 21 | 9a | ||
| 27 | mm2 | Pcc2 | P c c 2 | 5h | ||
| 28 | mm2 | Pma2 | P m a 2 | 6h | ||
| 29 | mm2 | Pca21 | P c a 21 | 11a | ||
| 30 | mm2 | Pnc2 | P n c 2 | 7h | ||
| 31 | mm2 | Pmn21 | P m n 21 | 10a | ||
| 32 | mm2 | Pba2 | P b a 2 | 9h | ||
| 33 | mm2 | Pna21 | P n a 21 | 12a | ||
| 34 | mm2 | Pnn2 | P n n 2 | 8h | ||
| 35 | mm2 | Cmm2 | C m m 2 | 14s | ||
| 36 | mm2 | Cmc21 | C m c 21 | 13a | ||
| 37 | mm2 | Ccc2 | C c c 2 | 10h | ||
| 38 | mm2 | Amm2 | A m m 2 | 15s | ||
| 39 | mm2 | Aem2 | A e m 2 | 11h | ||
| 40 | mm2 | Ama2 | A m a 2 | 12h | ||
| 41 | mm2 | Aea2 | A e a 2 | 13h | ||
| 42 | mm2 | Fmm2 | F m m 2 | 17s | ||
| 43 | mm2 | Fdd2 | F dd2 | 16h | ||
| 44 | mm2 | Imm2 | I m m 2 | 16s | ||
| 45 | mm2 | Iba2 | I b a 2 | 15h | ||
| 46 | mm2 | Ima2 | I m a 2 | 14h | ||
| 47 | Pmmm | P 2/m 2/m 2/m | 18s | |||
| 48 | Pnnn | P 2/n 2/n 2/n | 19h | |||
| 49 | Pccm | P 2/c 2/c 2/m | 17h | |||
| 50 | Pban | P 2/b 2/a 2/n | 18h | |||
| 51 | Pmma | P 21/m 2/m 2/a | 14a | |||
| 52 | Pnna | P 2/n 21/n 2/a | 17a | |||
| 53 | Pmna | P 2/m 2/n 21/a | 15a | |||
| 54 | Pcca | P 21/c 2/c 2/a | 16a | |||
| 55 | Pbam | P 21/b 21/a 2/m | 22a | |||
| 56 | Pccn | P 21/c 21/c 2/n | 27a | |||
| 57 | Pbcm [4] | P 2/b 21/c 21/m | 23a | |||
| 58 | Pnnm | P 21/n 21/n 2/m | 25a | |||
| 59 | Pmmn | P 21/m 21/m 2/n | 24a | |||
| 60 | Pbcn | P 21/b 2/c 21/n | 26a | |||
| 61 | Pbca | P 21/b 21/c 21/a | 29a | |||
| 62 | Pnma [5] | P 21/n 21/m 21/a | 28a | |||
| 63 | Cmcm[6] | C 2/m 2/c 21/m | 18a | |||
| 64 | Cmce[7] | C 2/m 2/c 21/e | 19a | |||
| 65 | Cmmm | C 2/m 2/m 2/m | 19s | |||
| 66 | Cccm | C 2/c 2/c 2/m | 20h | |||
| 67 | Cmme | C 2/m 2/m 2/e | 21h | |||
| 68 | Ccce | C 2/c 2/c 2/e | 22h | |||
| 69 | Fmmm | F 2/m 2/m 2/m | 21s | |||
| 70 | Fddd | F 2/d 2/d 2/d | 24h | |||
| 71 | Immm | I 2/m 2/m 2/m | 20s | |||
| 72 | Ibam | I 2/b 2/a 2/m | 23h | |||
| 73 | Ibca | I 2/b 2/c 2/a | 21a | |||
| 74 | Imma | I 2/m 2/m 2/a | 20a |
Liste des groupes tétragonaux
[modifier | modifier le code]| Primitif (tP) |
Centré (tI) |
|---|---|

|

|
| Numéro | Groupe ponctuel | Symbole abrégé | Symbole complet | Schoenflies | Fedorov | Shubnikov |
|---|---|---|---|---|---|---|
| 75 | 4 | P4 | P 4 | 22s | ||
| 76 | 4 | P41 | P 41 | 30a | ||
| 77 | 4 | P42 | P 42 | 33a | ||
| 78 | 4 | P43 | P 43 | 31a | ||
| 79 | 4 | I4 | I 4 | 23s | ||
| 80 | 4 | I41 | I 41 | 32a | ||
| 81 | 4 | P4 | P 4 | 26s | ||
| 82 | 4 | I4 | I 4 | 27s | ||
| 83 | 4/m | P4/m | P 4/m | 28s | ||
| 84 | 4/m | P42/m | P 42/m | 41a | ||
| 85 | 4/m | P4/n | P 4/n | 29h | ||
| 86 | 4/m | P42/n | P 42/n | 42a | ||
| 87 | 4/m | I4/m | I 4/m | 29s | ||
| 88 | 4/m | I41/a | I 41/a | 40a | ||
| 89 | 422 | P422 | P 4 2 2 | 30s | ||
| 90 | 422 | P4212 | P4212 | 43a | | |
| 91 | 422 | P4122 | P 41 2 2 | 44a | ||
| 92 | 422 | P41212 | P 41 21 2 | 48a | | |
| 93 | 422 | P4222 | P 42 2 2 | 47a | ||
| 94 | 422 | P42212 | P 42 21 2 | 50a | | |
| 95 | 422 | P4322 | P 43 2 2 | 45a | ||
| 96 | 422 | P43212 | P 43 21 2 | 49a | | |
| 97 | 422 | I422 | I 4 2 2 | 31s | ||
| 98 | 422 | I4122 | I 41 2 2 | 46a | ||
| 99 | 4mm | P4mm | P 4 m m | 24s | ||
| 100 | 4mm | P4bm | P 4 b m | 26h | ||
| 101 | 4mm | P42cm | P 42 c m | 37a | ||
| 102 | 4mm | P42nm | P 42 n m | 38a | ||
| 103 | 4mm | P4cc | P 4 c c | 25h | ||
| 104 | 4mm | P4nc | P 4 n c | 27h | ||
| 105 | 4mm | P42mc | P 42 m c | 36a | ||
| 106 | 4mm | P42bc | P 42 b c | 39a | ||
| 107 | 4mm | I4mm | I 4 m m | 25s | ||
| 108 | 4mm | I4cm | I 4 c m | 28h | ||
| 109 | 4mm | I41md | I 41 m d | 34a | ||
| 110 | 4mm | I41cd | I 41 c d | 35a | ||
| 111 | 42m | P42m | P 4 2 m | 32s | ||
| 112 | 42m | P42c | P 4 2 c | 30h | | |
| 113 | 42m | P421m | P 4 21 m | 52a | ||
| 114 | 42m | P421c | P 4 21 c | 53a | ||
| 115 | 42m | P4m2 | P 4 m 2 | 33s | ||
| 116 | 42m | P4c2 | P 4 c 2 | 31h | ||
| 117 | 42m | P4b2 | P 4 b 2 | 32h | ||
| 118 | 42m | P4n2 | P 4 n 2 | 33h | ||
| 119 | 42m | I4m2 | I 4 m 2 | 35s | ||
| 120 | 42m | I4c2 | I 4 c 2 | 34h | ||
| 121 | 42m | I42m | I 4 2 m | 34s | ||
| 122 | 42m | I42d | I 4 2 d | 51a | ||
| 123 | 4/m 2/m 2/m | P4/mmm | P 4/m 2/m 2/m | 36s | ||
| 124 | 4/m 2/m 2/m | P4/mcc | P 4/m 2/c 2/c | 35h | ||
| 125 | 4/m 2/m 2/m | P4/nbm | P 4/n 2/b 2/m | 36h | ||
| 126 | 4/m 2/m 2/m | P4/nnc | P 4/n 2/n 2/c | 37h | ||
| 127 | 4/m 2/m 2/m | P4/mbm | P 4/m 21/b 2/m | 54a | ||
| 128 | 4/m 2/m 2/m | P4/mnc | P 4/m 21/n 2/c | 56a | ||
| 129 | 4/m 2/m 2/m | P4/nmm | P 4/n 21/m 2/m | 55a | ||
| 130 | 4/m 2/m 2/m | P4/ncc | P 4/n 21/c 2/c | 57a | ||
| 131 | 4/m 2/m 2/m | P42/mmc | P 42/m 2/m 2/c | 60a | ||
| 132 | 4/m 2/m 2/m | P42/mcm | P 42/m 2/c 2/m | 61a | ||
| 133 | 4/m 2/m 2/m | P42/nbc | P 42/n 2/b 2/c | 63a | ||
| 134 | 4/m 2/m 2/m | P42/nnm | P 42/n 2/n 2/m | 62a | ||
| 135 | 4/m 2/m 2/m | P42/mbc | P 42/m 21/b 2/c | 66a | ||
| 136 | 4/m 2/m 2/m | P42/mnm | P 42/m 21/n 2/m | 65a | ||
| 137 | 4/m 2/m 2/m | P42/nmc | P 42/n 21/m 2/c | 67a | ||
| 138 | 4/m 2/m 2/m | P42/ncm | P 42/n 21/c 2/m | 65a | ||
| 139 | 4/m 2/m 2/m | I4/mmm | I 4/m 2/m 2/m | 37s | ||
| 140 | 4/m 2/m 2/m | I4/mcm | I 4/m 2/c 2/m | 38h | ||
| 141 | 4/m 2/m 2/m | I41/amd | I 41/a 2/m 2/d | 59a | ||
| 142 | 4/m 2/m 2/m | I41/acd | I 41/a 2/c 2/d | 58a |
Liste des groupes trigonaux
[modifier | modifier le code]| Rhomboédrique (hR) |
Hexagonal (hP) |
|---|---|

|

|
| Numéro | Groupe ponctuel | Symbole abrégé | Symbole complet | Schoenflies | Fedorov | Shubnikov |
|---|---|---|---|---|---|---|
| 143 | 3 | P3 | P 3 | 38s | ||
| 144 | 3 | P31 | P 31 | 68a | ||
| 145 | 3 | P32 | P 32 | 69a | ||
| 146 | 3 | R3 | R 3 | 39s | ||
| 147 | 3 | P3 | P 3 | 51s | ||
| 148 | 3 | R3 | R 3 | 52s | ||
| 149 | 32 | P312 | P 3 1 2 | 45s | ||
| 150 | 32 | P321 | P 3 2 1 | 44s | ||
| 151 | 32 | P3112 | P 31 1 2 | 72a | ||
| 152 | 32 | P3121 | P 31 2 1 | 70a | ||
| 153 | 32 | P3212 | P 32 1 2 | 73a | ||
| 154 | 32 | P3221 | P 32 2 1 | 71a | ||
| 155 | 32 | R32 | R 3 2 | 46s | ||
| 156 | 3m | P3m1 | P 3 m 1 | 40s | ||
| 157 | 3m | P31m | P 3 1 m | 41s | ||
| 158 | 3m | P3c1 | P 3 c 1 | 39h | ||
| 159 | 3m | P31c | P 3 1 c | 40h | ||
| 160 | 3m | R3m | R 3 m | 42s | ||
| 161 | 3m | R3c | R 3 c | 41h | ||
| 162 | 3 2/m | P31m | P 3 1 2/m | 56s | ||
| 163 | 3 2/m | P31c | P 3 1 2/c | 46h | ||
| 164 | 3 2/m | P3m1 | P 3 2/m 1 | 55s | ||
| 165 | 3 2/m | P3c1 | P 3 2/c 1 | 45h | ||
| 166 | 3 2/m | R3m | R 3 2/m | 57s | ||
| 167 | 3 2/m | R3c | R 3 2/c | 47h |
Liste des groupes hexagonaux
[modifier | modifier le code]
|
| Numéro | Groupe ponctuel | Symbole abrégé | Symbole complet | Schoenflies | Fedorov | Shubnikov |
|---|---|---|---|---|---|---|
| 168 | 6 | P6 | P 6 | 49s | ||
| 169 | 6 | P61 | P 61 | 74a | ||
| 170 | 6 | P65 | P 65 | 75a | ||
| 171 | 6 | P62 | P 62 | 76a | ||
| 172 | 6 | P64 | P 64 | 77a | ||
| 173 | 6 | P63 | P 63 | 78a | ||
| 174 | 6 | P6 | P 6 | 43s | ||
| 175 | 6/m | P6/m | P 6/m | 53s | ||
| 176 | 6/m | P63/m | P 63/m | 81a | ||
| 177 | 622 | P622 | P 6 2 2 | 54s | ||
| 178 | 622 | P6122 | P 61 2 2 | 82a | ||
| 179 | 622 | P6522 | P 65 2 2 | 83a | ||
| 180 | 622 | P6222 | P 62 2 2 | 84a | ||
| 181 | 622 | P6422 | P 64 2 2 | 85a | ||
| 182 | 622 | P6322 | P 63 2 2 | 86a | ||
| 183 | 6mm | P6mm | P 6 m m | 50s | ||
| 184 | 6mm | P6cc | P 6 c c | 44h | ||
| 185 | 6mm | P63cm | P 63 c m | 80a | ||
| 186 | 6mm | P63mc | P 63 m c | 79a | ||
| 187 | 6m2 | P6m2 | P 6 m 2 | 48s | ||
| 188 | 6m2 | P6c2 | P 6 c 2 | 43h | ||
| 189 | 6m2 | P62m | P 6 2 m | 47s | ||
| 190 | 6m2 | P62c | P 6 2 c | 42h | ||
| 191 | 6/m 2/m 2/m | P6/mmm | P 6/m 2/m 2/m | 58s | ||
| 192 | 6/m 2/m 2/m | P6/mcc | P 6/m 2/c 2/c | 48h | ||
| 193 | 6/m 2/m 2/m | P63/mcm | P 63/m 2/c 2/m | 87a | ||
| 194 | 6/m 2/m 2/m | P63/mmc | P 63/m 2/m 2/c | 88a |
Liste des groupes cubiques
[modifier | modifier le code]| Primitif (cP) |
Centré (cI) |
Faces centrées (cF) |
|---|---|---|

|

|

|



| Numéro | Groupe ponctuel | Symbole abrégé | Symbole complet | Schoenflies | Fedorov | Shubnikov | Fibrifold |
|---|---|---|---|---|---|---|---|
| 195 | 23 | P23 | P 2 3 | 59s | 2o | ||
| 196 | 23 | F23 | F 2 3 | 61s | 1o | ||
| 197 | 23 | I23 | I 2 3 | 60s | 4oo | ||
| 198 | 23 | P213 | P 21 3 | 89a | 1o/4 | ||
| 199 | 23 | I213 | I 21 3 | 90a | 2o/4 | ||
| 200 | 2/m 3 | Pm3 | P 2/m 3 | 62s | 4− | ||
| 201 | 2/m 3 | Pn3 | P 2/n 3 | 49h | 4+o | ||
| 202 | 2/m 3 | Fm3 | F 2/m 3 | 64s | 2− | ||
| 203 | 2/m 3 | Fd3 | F 2/d 3 | 50h | 2+o | ||
| 204 | 2/m 3 | Im3 | I 2/m 3 | 63s | 8−o | ||
| 205 | 2/m 3 | Pa3 | P 21/a 3 | 91a | 2−/4 | ||
| 206 | 2/m 3 | Ia3 | I 21/a 3 | 92a | 4−/4 | ||
| 207 | 432 | P432 | P 4 3 2 | 68s | 4−o | ||
| 208 | 432 | P4232 | P 42 3 2 | 98a | 4+ | ||
| 209 | 432 | F432 | F 4 3 2 | 70s | 2−o | ||
| 210 | 432 | F4132 | F 41 3 2 | 97a | 2+ | ||
| 211 | 432 | I432 | I 4 3 2 | 69s | 8+o | ||
| 212 | 432 | P4332 | P 43 3 2 | 94a | 2+/4 | ||
| 213 | 432 | P4132 | P 41 3 2 | 95a | 2+/4 | ||
| 214 | 432 | I4132 | I 41 3 2 | 96a | 4+/4 | ||
| 215 | 43m | P43m | P 4 3 m | 65s | 2o:2 | ||
| 216 | 43m | F43m | F 4 3 m | 67s | 1o:2 | ||
| 217 | 43m | I43m | I 4 3 m | 66s | 4o:2 | ||
| 218 | 43m | P43n | P 4 3 n | 51h | 4o | ||
| 219 | 43m | F43c | F 4 3 c | 52h | 2oo | ||
| 220 | 43m | I43d | I 4 3 d | 93a | 4o/4 | ||
| 221 | 4/m 3 2/m | Pm3m | P 4/m 3 2/m | 71s | 4−:2 | ||
| 222 | 4/m 3 2/m | Pn3n | P 4/n 3 2/n | 53h | 8oo | ||
| 223 | 4/m 3 2/m | Pm3n | P 42/m 3 2/n | 102a | 8o | ||
| 224 | 4/m 3 2/m | Pn3m | P 42/n 3 2/m | 103a | 4+:2 | ||
| 225 | 4/m 3 2/m | Fm3m | F 4/m 3 2/m | 73s | 2−:2 | ||
| 226 | 4/m 3 2/m | Fm3c | F 4/m 3 2/c | 54h | 4−− | ||
| 227 | 4/m 3 2/m | Fd3m | F 41/d 3 2/m | 100a | 2+:2 | ||
| 228 | 4/m 3 2/m | Fd3c | F 41/d 3 2/c | 101a | 4++ | ||
| 229 | 4/m 3 2/m | Im3m | I 4/m 3 2/m | 72s | 8o:2 | ||
| 230 | 4/m 3 2/m | Ia3d | I 41/a 3 2/d | 99a | 8o/4 |
Notes et références
[modifier | modifier le code]- (en) [PDF] Symmetry Operations and Space Groups sur chemistry.bd.psu.edu, consulté le 17/02/2017.
- parfois noté C1
- ou P21/a, P21/n
- parfois noté I2/a ou C2/n
- ou Pbnm
- ou Pnam
- ou Ccmm
- ou Cmca






















































































































































































































































































































































































































































































