Cercles inscrit et exinscrits d'un triangle

Les trois cercles exinscrits d'un triangle et son cercle inscrit.

Étant donnés trois points non alignés A, B et C du plan, il existe quatre cercles tangents aux trois droites (AB), (AC) et (BC). Ce sont le cercle inscrit (celui qui est intérieur au triangle) et les cercles exinscrits du triangle ABC.

Bissectrices

Bissectrices et cercle inscrit d'un triangle.

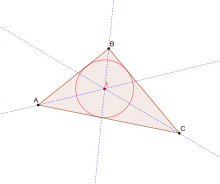
Un cercle tangent aux trois droites (AB), (BC), (CA) doit posséder un centre équidistant de ces trois droites. Or l'ensemble des points équidistants de deux droites sécantes (d₁) et (d₂) forme deux droites perpendiculaires, constituées des quatre demi-droites bissectrices chacune d'un des quatre secteurs angulaires construits par les droites (d₁) et (d₂), et appelées bissectrices des droites (d₁) et (d₂).

Si on considère les trois côtés du triangle en tant que droites, on dispose en tout de six bissectrices, deux pour chaque couple de droites. Par chacun des sommets du triangle, passe une bissectrice intérieure (qui rencontre le côté opposé du triangle) et une bissectrice extérieure.

Si une bissectrice issue de A rencontre une bissectrice issue de B alors le point d'intersection, étant équidistant de (AB) et (AC) et équidistant de (BA) et (BC), est à égale distance de (CA) et (CB) et appartient donc à l'une (et une seule) des bissectrices issues de C. Il y a donc quatre points de concours possibles.

Cas du cercle inscrit. Les bissectrices intérieures issues de A et B se coupent à l'intérieur des secteurs angulaires (BAC) et (ABC), c'est-à-dire dans le triangle ABC. Le point d'intersection est donc sur la bissectrice intérieure issue de C et plus exactement sur la demi-droite bissectrice du secteur angulaire (ACB). Le point d'intersection est alors le centre d'un cercle tangent aux trois côtés du triangle. C'est le cercle inscrit.

Cas des cercles exinscrits. Les bissectrices extérieures issues de A et de B se coupent dans le secteur angulaire (ACB) et rencontrent donc, eux aussi, la demi-droite bissectrice de l'angle (ACB). Le point d'intersection est alors le centre d'un cercle tangent au segment [AB] et aux demi-droites d'origines A et B, de supports (AC) et (BC) et ne contenant pas C. C'est un cercle exinscrit au triangle. Un raisonnement analogue peut être fait pour les deux autres couples de bissectrices extérieures.

Le cercle inscrit et les trois cercles exinscrits sont parfois appelés les quatre cercles tritangents du triangle.

Notations

Notations utilisées dans cet article

Dans cet article, a désigne la longueur du côté [BC], b la longueur du côté [AC] et c la longueur du côté [AB]. Enfin O désigne le centre du cercle inscrit et O_A, O_B et O_C les trois centres des cercles exinscrits compris dans les secteurs angulaires issus respectivement de A, B, C.

Cercle inscrit

Il existe un et un seul cercle intérieur au triangle et tangent à la fois à ses trois côtés. Ce cercle est appelé « cercle inscrit » dans le triangle. C'est le plus grand cercle que peut contenir ce triangle.

Centre

Son centre est le point d'intersection des bissectrices ; par définition, ses coordonnées trilinéaires par rapport aux sommets sont donc 1 : 1 : 1 et c'est le barycentre du système ${\textstyle {\begin{pmatrix}A&B&C\\a&b&c\end{pmatrix}}}$. C'est le premier centre X(1) répertorié dans l'ETC.

Les distances $d_{A},d_{B},d_{C}$ du centre du cercle inscrit aux sommets sont données par $d_{A}={\frac {bc}{p}}\cos {\frac {\widehat {A}}{2}}$ ou $d_{A}^{2}={\frac {p-a}{p}}bc$ et les formules permutées.

La relation d'Euler donne la distance d du centre du cercle inscrit au centre du cercle circonscrit : d² = R² - 2Rr (avec R rayon du cercle circonscrit, r celui du cercle inscrit) .

Rayon

S = a.r/2 + b.r/2 + c.r/2 = p.r

Le rayon du cercle inscrit est égal, d'après la preuve illustrée ci-contre, à

$r={\frac {S}{p}}={\frac {2S}{a+b+c}}$

où S désigne l'aire du triangle et p = a + b + c/2 son demi-périmètre.

Donc ${\frac {1}{r}}={\frac {1}{h_{A}}}+{\frac {1}{h_{B}}}+{\frac {1}{h_{C}}}$ où $h_{A}={\frac {2S}{a}},h_{B}={\frac {2S}{b}},h_{C}={\frac {2S}{c}}$ sont les trois hauteurs du triangle : le rayon du cercle inscrit est le tiers de leur moyenne harmonique.

Compte-tenu de la formule de Héron, on obtient :

$r^{2}={\frac {(p-a)(p-b)(p-c)}{p}}={\frac {(a+b-c)(a-b+c)(-a+b+c)}{4(a+b+c)}}.$

$T_{A},T_{B},T_{C}$ étant les points de contact du cercle inscrit avec les côtés $[BC],[CA],[AB]$, les distances des points de contact aux sommet, appelées "distances de contact", sont $x=AT_{B}=AT_{C},y=BT_{C}=BT_{A},z=CT_{A}=CT_{B}$.

Comme a = y+z, b = z+x, c = x+y , on obtient :

x = p – a, y = p – b, z = p – c,

d'où :

$r^{2}={\frac {xyz}{x+y+z}}$.

D'autre part, si l'on se souvient que ${\frac {abc}{2S}}=2R$, où $R$ désigne le rayon du cercle circonscrit au même triangle,

on a :

$Rr={\frac {abc}{2(a+b+c)}}$.

Dans le cas du triangle rectangle d'hypoténuse de longueur $c$, l'expression du rayon se simplifie en $r={\frac {a+b-c}{2}}$.

Point de Gergonne

G_e est le point de Gergonne du triangle ABC.

D'après le théorème de Ceva, les trois céviennes $(AT_{A}),(BT_{B}),(CT_{C})$ joignant les sommets aux points de contact, sont concourantes. En effet, le produit des rapports ${\frac {T_{C}A}{T_{C}B}}\times {\frac {T_{A}B}{T_{A}C}}\times {\frac {T_{B}C}{T_{B}A}}={\frac {x}{y}}{\frac {y}{z}}{\frac {z}{x}}$ est égal à 1.

Leur point de concours est appelé le point de Gergonne du triangle et le triangle T_AT_BT_C, le triangle de contact (ou triangle de Gergonne) du triangle ABC.

Ses coordonnées barycentriques dans ABC sont $\left({\frac {1}{x}}:{\frac {1}{y}}:{\frac {1}{z}}\right)=\left({\frac {1}{-a+b+c}}:{\frac {1}{a-b+c}}:{\frac {1}{a+b-c}}\right)$.

Démonstration

Si X est le point de coordonnées barycentriques $\left({\frac {1}{x}}:{\frac {1}{y}}:{\frac {1}{z}}\right)$, le point d'intersection $X_{A}$ de (AX) et (BC) vérifie ${\frac {1}{y}}{\overline {X_{A}B}}+{\frac {1}{z}}{\overline {X_{A}C}}=0$, soit ${\frac {\overline {X_{A}C}}{\overline {X_{A}B}}}={\frac {z}{y}}$, donc $X_{A}=T_{A}$ et de même $X_{B}=T_{B}$, $X_{C}=T_{C}$ ; donc X est le point de Gergonne.

il est répertorié X(7) dans l'ETC.

De plus, Si T'_A est le point d'intersection des droites (T_BT_C) et (BC) , les points T'_A, B, T_A et C sont en division harmonique.

Propriétés du triangle de contact

Les angles en vert sont tous égaux.

• L'angle à l'un des sommets du triangle de Gergonne est égal à l'angle entre les deux bissectrices issues des sommets du triangle initial formant le côté où se trouve le sommet du triangle de Gergonne.

Les intersections des bissectrices avec les côtés du triangle de contact présentent des caractéristiques particulières.

• Les points d'intersection des bissectrices avec les côtés du triangle de contact permettent de construire trois droites orthogonales aux bissectrices.

Un triangle et sa droite de Gergonne.

• Un triangle et son triangle de contact sont homologiques, de centre le conjugué isogonal du point de Gergonne pour le triangle de référence (nombre de Kimberling X₅₅) et d'axe une droite appelée droite de Gergonne du triangle de référence. Les points d'intersection de l'homologie sont les points de Nobbs, qui sont donc par définition sur la droite de Gergonne, de même de que les points de Fletcher et d'Evans du triangle de référence.

Cercle inscrit dans le triangle médian

Le centre du cercle inscrit dans le triangle médian est le centre de gravité de la ligne homogène ABCA.

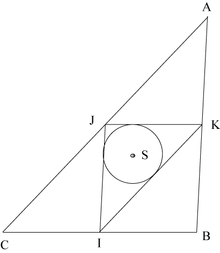
Le centre du cercle inscrit dans le triangle médian IJK (I milieu de [BC], etc.), appelé point de Spieker, est le centre de gravité (ou d'inertie) de la ligne polygonale homogène formée par les côtés du triangle.

C'est en effet le barycentre du système ${\textstyle {\begin{pmatrix}I&J&K\\a&b&c\end{pmatrix}}}$ ; ses coordonnées barycentriques dans le triangle de départ sont donc $(b+c:c+a:a+b)$ ; il est répertorié X(10) dans l'ETC.

Cercles exinscrits

Aire de $ABC$ = aire de $AI_{A}C$+aire de $AI_{A}B$ - aire de $I_{A}BC$ . Donc, $S={\frac {1}{2}}(br_{A}+cr_{A}-ar_{A})$, d'où $r_{A}={\frac {S}{p-a}}$.

Il y a trois cercles exinscrits : chacun est tangent à un unique côté du triangle (considéré comme un segment). On note C_A le cercle exinscrit touchant le côté [CB], C_B le cercle exinscrit touchant le côté [AC] et C_C le cercle exinscrit touchant le côté [AB].

Les rayons des cercles exinscrits sont respectivement (démonstration ci-contre) : $r_{A}={\frac {S}{p-a}},\quad r_{B}={\frac {S}{p-b}}\quad {\rm {et}}\quad r_{C}={\frac {S}{p-c}}$ donc

${\frac {1}{r_{A}}}+{\frac {1}{r_{B}}}+{\frac {1}{r_{C}}}={\frac {p}{S}}={\frac {1}{r}}$

et $S={\sqrt {r_{A}r_{B}r_{C}r}}$.

De plus, le rayon du cercle circonscrit est donné par $R=r_{A}+r_{B}+r_{C}-r$ .

On peut noter les relations : ${\frac {r_{A}}{r}}={\frac {p}{p-a}}={\frac {h_{A}}{h_{A}-2r}}={\frac {\tan({\widehat {B}}+{\widehat {C}})}{\tan {\widehat {A}}}}$, où $h_{A}$ est la hauteur issue de $A$.

Leurs centres sont barycentres du système ${\textstyle {\begin{pmatrix}A&B&C\\-a&b&c\end{pmatrix}}}$ pour le premier, ${\textstyle {\begin{pmatrix}A&B&C\\a&-b&c\end{pmatrix}}}$ pour le second et ${\textstyle {\begin{pmatrix}A&B&C\\a&b&-c\end{pmatrix}}}$ pour le troisième.

Le terme "exinscrit" a été introduit par Simon Antoine Jean L'Huillier.

Le triangle formé par les centres des trois cercles exinscrits est également appelé triangle exinscrit, ou aussi triangle excentral ou triangle de Bevan.

Point de Nagel

Point de Nagel d'un triangle.

Notons U_A le point de contact de C_A avec [CB], U_B le point de contact de C_B avec [AC] et U_C le point de contact de C_C avec [AB].

Alors les droites (AU_A), (BU_B) et (CU_C) sont concourantes : leur point d'intersection N_a s'appelle le point de Nagel du triangle. On appelle le triangle U_AU_BU_C le triangle de Nagel du triangle ABC.

Le point de Nagel N_a, le centre du cercle inscrit I et le centre de gravité G sont alignés sur la droite de Nagel et liés par la relation IN_a = 3 IG. Le point de Spieker est aussi sur cette droite, c'est le centre du cercle inscrit dans le triangle médian.

Il est possible de construire en quelques secondes le point de Nagel d'un triangle en s'inspirant d'une construction qui aboutit au cercle de Conway.

Point de Bevan

Point et triangle de Bevan.

Les droites (O_AU_A), (O_BU_B) et (O_CU_C) sont également concourantes : leur point d'intersection B_e s'appelle le point de Bevan du triangle ABC (portant le nom de Benjamin Bevan) et le triangle O_AO_BO_C s'appelle le triangle de Bevan de ABC.

Le point de Bevan est le symétrique du centre du cercle inscrit dans ABC, par rapport au centre du cercle circonscrit à ABC. Le point de Bevan et ces deux centres sont donc alignés.

Le point de Bevan est le centre du cercle circonscrit au triangle de Bevan.

Le triangle de Bevan et le triangle de Gergonne sont homothétiques.

Point d'Apollonius

Point d'Apollonius d'un triangle.

Il existe un unique cercle tangent simultanément aux trois cercles exinscrits et qui les contienne (voir Problème des contacts) ; c'est le cercle d'Apollonius du triangle. Si l'on note V_A, V_B et V_C les trois points de tangence alors les droites (AV_A), (BV_B) et (CV_C) sont concourantes : leur point d'intersection A_p s'appelle le point d'Apollonius du triangle.

Mittenpunkt

Le mittenpunkt d'un triangle ABC

On appelle mittenpunkt du triangle ABC le point de concours des droites reliant les centres O_A, O_B, O_C des trois cercles exinscrits aux milieux respectifs des côtés du triangle.

Le mittenpunkt M_i est situé sur la droite reliant le centre de gravité G au point de Gergonne G_e avec la relation M_iG_e= 3M_iG.

Le mittenpunkt M_i est situé sur la droite reliant le centre du cercle inscrit au point de Lemoine . 

Le mittenpunkt est également le point de Lemoine du triangle de Bevan O_AO_BO_C, triangle formé par les bissectrices extérieures, de sommets les centres des trois cercles exinscrits.

Le mittenpunkt d'un triangle est le centre de son ellipse de Mandart.

Il est le centre de l'ellipse de Mandart du triangle (l'ellipse inscrite dans le triangle et tangente aux points de contact des cercles exinscrits U_A, U_B, U_C).

Points de Feuerbach

Triangle de Feuerbach.

Les trois cercles exinscrits et le cercle inscrit sont tangents au cercle d'Euler du triangle ABC. Les points de contact F^e, Fe
A, Fe
B, Fe
C de ces cercles s'appellent les points de Feuerbach du triangle. Ce résultat constitue le théorème de Feuerbach.

Les trois points de tangence des cercles exinscrits forment le triangle de Feuerbach Fe
AFe
BFe
C du triangle ABC.

Le point S, les centres I et J et le point de Feuerbach Fe sont alignés.

Soit S le point de concours des droites (AFe
A), (BFe
B), (CFe
C). Alors le point S, le centre du cercle inscrit, le centre du cercle d'Euler et le point de Feuerbach F^e sont alignés et en division harmonique.

Le cercle, circonscrit au triangle formé par les pieds des bissectrices, passe par le point de Feuerbach F^e.

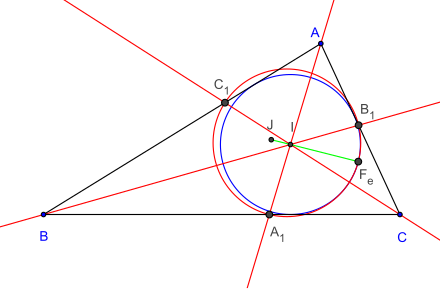
Le cercle passant par les pieds des bissectrices intérieures du triangle ABC passe aussi par le point de Feuerbach F^e.

Hyperbole de Feuerbach.

Le point de Feuerbach F^e est le centre de symétrie d'une hyperbole équilatère (dite hyperbole de Feuerbach) passant en particulier par :

• les trois sommets du triangle ;
• l'orthocentre ;
• le centre du cercle inscrit ;
• le point de Gergonne ;
• le point de Nagel ;
• le mittenpunkt.

Le point de Feuerbach d'un triangle est le seul centre de ce triangle à être sur son ellipse de Mandart

Le point de Feuerbach est un des seuls centres du triangle sur l'ellipse de Mandart (ellipse tangente aux côtés du triangle aux points de contact des cercles exinscrits et ayant pour centre le mittenpunkt).

Notes et références

• Yvonne et René Sortais, La géométrie du triangle, Hermann, 1997 (ISBN 978-2-7056-1429-4).
• Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009 (ISBN 978-2-91-635208-4).

Voir aussi

Articles connexes

• Cercle circonscrit au triangle
• Nombre de Kimberling
• Triplet pythagoricien ; le triangle associé possède des cercles inscrits et exinscrits très simples
• Carré inscrit dans un triangle

Liens externes

• (en) A. Bogomolny, « Incircles and Excircles in a Triangle », sur Cut The Knot
• (en) Eric W. Weisstein, « Incircle », sur MathWorld
• (en) Eric W. Weisstein, « Excircles », sur MathWorld
• (en) Eric W. Weisstein, « Nagel Point », sur MathWorld
• (en) Eric W. Weisstein, « Gergonne Point », sur MathWorld
• (en) Eric W. Weisstein, « Bevan Point », sur MathWorld
• (en) Eric W. Weisstein, « Mittenpunkt », sur MathWorld