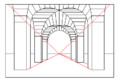
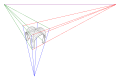
Punt de fuga

El punt de fuga és el lloc on convergeixen totes línies "paral·leles" de color verd, i la línia de l'horitzó, representada aquí com la recta horitzontal de color blau

Punt de fuga situat en l'horitzó

Un punt de fuga, en un sistema de projecció cònica, és el lloc geomètric en el qual convergeixen les projeccions de les rectes paral·leles en una direcció donada en l'espai, no paral·leles al pla de projecció. És un punt situat en l'infinit. Existeixen tants punts de fuga com direccions en l'espai. Un punt de fuga corresponent a una direcció donada en l'espai queda definit mitjançant la intersecció entre el pla de projecció i un raig, amb aquesta direcció, traçat des de l'origen (o punt de vista).

Un exemple intuïtiu de punt de fuga és el lloc on "veuríem confluir" els dos rails d'una via rectilínia de tren disposada sobre un terreny pla infinit.

Punts de fuga definits

En una projecció donada, es poden determinar d'un a tres punts de fuga per representar les tres direccions ortogonals corresponents als tres eixos espacials XYZ, segons es mantinguin paral·leles al pla de projecció o s'intersequin amb aquest. Aquests tres eixos es poden imaginar com les arestes d'un ortoedre o un cub.

En funció de les direccions dels eixos ortogonals respecte al pla de projecció, les perspectives es denominen:

• Perspectiva frontal: amb un sol punt de fuga sobre el dibuix. Ocorre quan una de les cares del cub és paral·lela al pla de projecció; per tant, dos eixos de l'espai són paral·lels al pla de projecció. Les projeccions de les rectes en aquestes direccions es veuran realment paral·leles en el dibuix.
• Perspectiva obliqua: amb dos punts de fuga. Ocorre quan el cub està parcialment de costat, i només un eix espacial és paral·lel al pla de projecció. Les rectes amb aquesta direcció es projecten realment paral·leles en el dibuix.
• Perspectiva aèria: amb tres punts de fuga. Ocorre quan el cub està parcialment de costat i bolcat. Cap direcció ortogonal és paral·lela al pla de projecció.

En el sistema de projecció cònica, les projeccions de les rectes horitzontals convergeixen sempre en la línia de l'horitzó; i solament les projeccions de les rectes paral·leles al pla del quadre no tenen un punt de fuga definit, puix també es projecten realment paral·leles en el dibuix.

• 
  Un punt de fuga central. Vista frontal
• 
  Dos punts de fuga. Vista obliqua
• 
  Tres punts de fuga. Vista aèria

Altura del punt de vista

Vistes amb dos punts de fuga

La distància existent entre l'observador i el pla geometral es veu reflectida en l'altura h (distància entre la L. H. i la L.T.). La visió que s'obté de l'objecte difereix notablement amb la situació del punt de vista, com s'observa en la il·lustració. En aquest tipus de representacions, tant d'interiors com d'exteriors, s'estableix, normalment, una altura per a la línia de l'horitzó (aproximadament, la mitjana d'una persona) 1,70 o 1,20 metres, segons es consideri dempeus o asseguda. Un punt de vista baix (perspectiva de granota) mostra una menor proporció del pla de terra, alhora que disminueix la distància entre la línia de l'horitzó i la de terra. Amb aquest tipus de perspectiva, s'aconsegueix ressaltar l'altura dels objectes. La representació de conjunts arquitectònics a “vista d'ocell” és molt emprada per oferir clarament la distribució urbanística. En aquest cas, la L. H. s'eleva molt per sobre de la L. T. En la vista celeste, se situa la L.T. per sobre de la L. H., de manera que puguem visualitzar la planta inferior de l'objecte.

Vegeu també

• Perspectiva
• Perspectiva cònica

Enllaços externs

• Representació de perspectiva basada en punts de fuga Arxivat 2015-11-17 a Wayback Machine..
• Exercicis de perspectiva cònica. (castellà)
• Càlcul trigonomètric dels punts de fuga. Explicació breu del principi amb un exemple fàcil (anglès)(alemany)