Wielościan półforemny
Wielościan półforemny, wielościan archimedesowy[1] – wielościan spełniający co najmniej trzy warunki:
- jego ściany są foremne;
- w każdym wierzchołku zbiega się jednakowa liczba ścian;
- istnieje izometria przekształcająca każdy wierzchołek na każdy inny (warunek wierzchołkowej tranzytywności)[2][a].
Jest to uogólnienie wielościanów foremnych (brył platońskich) – wielościany archimedesowe nie mają warunku przystawania ścian. Czasem definiuje się je wężej, wykluczając z nich bryły platońskie[potrzebny przypis].
Istnieje 13 wielościanów półforemnych (15 jeśli liczyć odbicia lustrzane dwóch spośród nich) oraz dwie nieskończone serie.
Nazwa pochodzi od imienia Archimedesa z Syrakuz[potrzebny przypis].
Nieskończone serie
[edytuj | edytuj kod]- graniastosłupy archimedesowe
- antygraniastosłupy
Pozostałe wielościany półforemne
[edytuj | edytuj kod]| Nazwa (Konfiguracja wektorowa) |
Grafika przejrzysta | Grafika nieprzejrzysta | Siatka | Ściany | Krawędzie | Wierzchołki | Grupa symetryczna | |
|---|---|---|---|---|---|---|---|---|
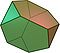
| Czworościan ścięty (3.6.6) |
 |
|
|
8 | 4 trójkąty 4 sześciokąty |
18 | 12 | Td |
| Sześcio-ośmiościan (3.4.3.4) |
 |
|
|
14 | 8 trójkątów 6 kwadratów |
24 | 12 | Oh |
| Sześcian ścięty (3.8.8) |
 |
|
|
14 | 8 trójkątów 6 ośmiokątów |
36 | 24 | Oh |
| Ośmiościan ścięty (4.6.6) |
 |
|
|
14 | 6 kwadratów 8 sześciokątów |
36 | 24 | Oh |
| Sześcio-ośmiościan rombowy mały (3.4.4.4) |
 |
|
|
26 | 8 trójkątów 18 kwadratów |
48 | 24 | Oh |
| Sześcio-ośmiościan rombowy wielki (4.6.8) |
 |
|
|
26 | 12 kwadratów 8 sześciokątów 6 ośmiokątów |
72 | 48 | Oh |
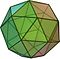
| Sześcio-ośmiościan przycięty (3.3.3.3.4) |
  |
|
|
38 | 32 trójkąty 6 kwadratów |
60 | 24 | O |
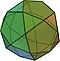
| Dwudziesto-dwunastościan (3.5.3.5) |
 |
 
|
|
32 | 20 trójkątów 12 pięciokątów |
60 | 30 | Ih |
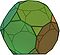
| Dwunastościan ścięty (3.10.10) |
 |
|
|
32 | 20 trójkątów 12 dziesięciokątów |
90 | 60 | Ih |
| Dwudziestościan ścięty (5.6.6) |
 |
|
|
32 | 12 pięciokątów 20 sześciokątów |
90 | 60 | Ih |
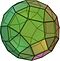
| Dwudziesto-dwunastościan rombowy mały (3.4.5.4) |
 |
|
|
62 | 20 trójkątów 30 kwadratów 12 pięciokątów |
120 | 60 | Ih |
| Dwudziesto-dwunastościan rombowy wielki (4.6.10) |
 |
|
|
62 | 30 kwadratów 20 sześciokątów 12 dziesięciokątów |
180 | 120 | Ih |
| Dwudziesto-dwunastościan przycięty (3.3.3.3.5) |
  |
|
|
92 | 80 trójkątów 12 pięciokątów |
150 | 60 | I |
Uwagi
[edytuj | edytuj kod]- ↑ Można spotkać definicje pozbawione warunku wierzchołkowej tranzytywności. Wówczas do wielościanów foremnych zaliczany jest również pseudo sześcio-ośmiościan rombowy mały[2].
Przypisy
[edytuj | edytuj kod]- ↑ wielościan archimedesowy, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2021-10-02].
- ↑ a b Pseudo sześcio-ośmiościany rombowe. matematyka.wroc.pl, 2008-09-05. [dostęp 2015-06-25].
Linki zewnętrzne
[edytuj | edytuj kod]
Małgorzata Kantor-Szcześniak, Bryły archimedesowe, Zintegrowana Platforma Edukacyjna, zpe.gov.pl [dostęp 2024-05-20].- Eric W. Weisstein, Archimedean Solid, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2023-06-18].
| definiowane jakościowo |
| ||||||
|---|---|---|---|---|---|---|---|
| definiowane ilościowo | |||||||
| uogólnienia |
| pojęcia definiujące |
| ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| typy wielościanów |
| ||||||||||||||||
| relacje dwuczłonowe między wielościanem a |
| ||||||||||||||||
| twierdzenia | |||||||||||||||||
| uogólnienia |
