此条目的主題是数学名词角。关于与「
角 」標題相近或相同的条目,請見「
角 (消歧义) 」。
Unicode 中的角符號,碼位為U+2220 在几何学 中,角 ( jiǎo ) angle )或精确用语平面角 ,是由两条有公共端点的射线 组成的几何对象。这两条射线叫做角的边 ,它们的公共端点叫做角的顶点 。一般的角會假設在欧几里得平面 上,但在非欧几里得几何 中也可以定義角,特別是在球面幾何學 中的球面角 大圓 的圓弧代替射线。角在几何学 和三角学 中有着广泛的应用。
几何之父欧几里得 曾定义角为在平面 中两条不平行 的直线 的相对斜度。普罗克鲁斯 認為角可能是一種特質、一種可量化的量、或是一種關係。歐德謨 直線 的偏差,安提阿的卡布斯 [ 1]
平面角大小的计量单位制 常用的有360度制 、弧度制 等[ 2] [ 3]
角通常用三个字母表示:两条边上的点的字母写在两旁,顶点上的字母写在中间。图中的角用∠AOB或
A
O
B
^
{\displaystyle {\widehat {AOB}}}
在數學式中,一般會用希臘字母 (
α
,
β
,
γ
,
θ
,
φ
,
.
.
.
{\displaystyle \alpha ,\beta ,\gamma ,\theta ,\varphi ,...}
π 一般不用來表示角度。
以角的端点为圆心 做圆弧 。由于圆弧的半径 和弧长成正比 ,而角是长度的比例 ,所以圆的大小不会影响角的测量。
角度 角度 在天文学 和全球定位系统 中有重要应用。弧度 圆弧 的长度除以圆的半径,單位是rad(中文名:弳)。弧度在数学 中有广泛的应用。弧度 還是国际单位制 中规定的角的標準度量,但却不是中国法定计量单位,角度 则是角在中国的法定计量单位。採用弧度時,通常不會標示單位,例如:
sin
π
=
sin
180
∘
=
0
{\displaystyle \sin \pi =\sin 180^{\circ }=0}
百分度 角度的量測可以視為弧長s 和半徑r 的比例,再依選用單位乘以一比例係數
2
π
n
{\displaystyle {\frac {2\pi }{n}}}
θ
=
n
2
π
s
r
{\displaystyle \theta ={\frac {n}{2\pi }}{\frac {s}{r}}}
例如以上的弧度、角度和百分度,其轉換係數
n
{\displaystyle n}
2
π
{\displaystyle 2\pi }
以下是一些其他的测量单位,對應不同的
n
{\displaystyle n}
圈數或轉數 (
n
=
1
{\displaystyle n=1}
cyc 、rev 或rot ,不過在每分鐘轉速 (RPM)的單位中,只用一個字母r表示。
直角 (
n
=
4
{\displaystyle n=4}
1
4
{\displaystyle {\frac {1}{4}}}
幾何原本 中用的角度單位,直角
=
90
∘
=
π
2
r
a
d
=
1
4
t
u
r
n
=
100
g
r
a
d
{\displaystyle =90^{\circ }={\frac {\pi }{2}}\mathrm {rad} ={\frac {1}{4}}\mathrm {turn} =100\mathrm {grad} }
⌞
{\displaystyle \llcorner }
時角 (
n
=
24
{\displaystyle n=24}
天文學 中,是
1
24
{\displaystyle {\frac {1}{24}}}
角分 及角秒 不同,前者大小為後者的十五倍。1時角
=
15
∘
=
π
12
r
a
d
=
1
6
q
u
a
d
=
1
24
t
u
r
n
≈
16.667
g
r
a
d
{\displaystyle =15^{\circ }={\frac {\pi }{12}}\mathrm {rad} ={\frac {1}{6}}\mathrm {quad} ={\frac {1}{24}}\mathrm {turn} \approx 16.667\mathrm {grad} }
密位 (
n
=
6000
∼
6400
{\displaystyle n=6000\sim 6400}
弧度 的角度,有許多不同的定義,其數值從0.05625度到0.06度(3.375至3.6角分),而毫弧度約為0.05729578度(3.43775角分)。在北大西洋公約組織 的國家中,密位定義為圓的
1
6400
{\displaystyle {\frac {1}{6400}}}
2
π
6400
=
0.0009817...
≑
1
1000
{\displaystyle {\frac {2\pi }{6400}}=0.0009817...\doteqdot {\frac {1}{1000}}}
角分 (
n
=
21600
{\displaystyle n=21600}
1
60
{\displaystyle {\frac {1}{60}}}
1
21600
{\displaystyle {\frac {1}{21600}}}
3
+
30
60
{\displaystyle 3+{\frac {30}{60}}}
3
∘
5.72
′
=
3
+
5.72
60
{\displaystyle 3^{\circ }5.72'=3+{\frac {5.72}{60}}}
海里 曾定義為在地球的大圓 上一角分的弧長。角秒 (
n
=
1296000
{\displaystyle n=1296000}
1
60
{\displaystyle {\frac {1}{60}}}
3
+
7
60
+
30
3600
{\displaystyle 3+{\frac {7}{60}}+{\frac {30}{3600}}}
以上角的定義均未考慮數值為負的角。不過在一些應用時,會將角的數值加上正負號,以標明是相對參考物不同方向的旋轉。
在二維的笛卡兒坐標系 中,角一般是以x軸的正向為基準,若往y軸的正向旋轉,則其角為正角,若往y軸的負向旋轉,則其角為負角。若二維的笛卡兒坐標系也是x軸朝右,y軸朝上,則逆時針的旋轉對應正角,順時針 的旋轉對應負角。
一般而言,
−
θ
{\displaystyle -\theta }
θ
{\displaystyle \theta }
−
45
∘
{\displaystyle -45^{\circ }}
360
∘
−
45
∘
(
=
315
∘
)
{\displaystyle 360^{\circ }-45^{\circ }(=315^{\circ })}
−
45
∘
{\displaystyle -45^{\circ }}
在三維的幾何中,順時針及逆時針沒有絕對的定義,因此定義正角及負角時均需列出其參考的基準,一般會以一個通過角的頂點,和角所在平面垂直的向量 為基準。
在導航 時,導向 是以北方為基準,正向表示順時針,因此導向45°對應東北方。導向沒有負值,西北方對應的導向為315°。
除了量測角本身的大小外.也有其他的方式,可以量測角的大小。
坡度 等於一個角的正切值,常用百分比或千分比來表示。當一個角的坡度小於5%時,其坡度近似於角以弧度表示的數值。
在有理幾何學
零角
角度等於0°,或弧度為0的角。
锐角
角度大于0°且小于90°,或弧度大于0且小于
π
2
{\displaystyle {\frac {\pi }{2}}}
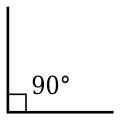
直角
角度等於90°,或弧度为
π
2
{\displaystyle {\frac {\pi }{2}}}
钝角
角度大于90°且小于180°,或弧度大于
π
2
{\displaystyle {\frac {\pi }{2}}}
π
{\displaystyle \pi }
平角
角度等於180°,或弧度为
π
{\displaystyle \pi }
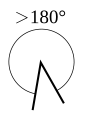
優角或反角
角度大於180°且小於360°,或弧度大於
π
{\displaystyle \pi }
2
π
{\displaystyle 2\pi }
周角
角度等於360°,或弧度為
2
π
{\displaystyle 2\pi }
直角
優角(或作反角)
周角
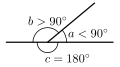
銳角(a )、鈍角(b )和平角(c )
以下是各角度的名稱及不同單位下的數值:
名稱
零角
銳角
直角
鈍角
平角
優角
周角
單位
範圍
轉
0
{\displaystyle 0}
(
0
,
1
4
)
{\displaystyle (0,{\tfrac {1}{4}})}
1
4
{\displaystyle {\tfrac {1}{4}}}
(
1
4
,
1
2
)
{\displaystyle ({\tfrac {1}{4}},{\tfrac {1}{2}})}
1
2
{\displaystyle {\tfrac {1}{2}}}
(
1
2
,
1
)
{\displaystyle ({\tfrac {1}{2}},1)}
1
{\displaystyle 1}
弧度
0
π
{\displaystyle 0\pi \,}
(
0
,
1
2
π
)
{\displaystyle (0,{\tfrac {1}{2}}\pi )}
1
2
π
{\displaystyle {\tfrac {1}{2}}\pi }
(
1
2
π
,
π
)
{\displaystyle ({\tfrac {1}{2}}\pi ,\pi )}
π
{\displaystyle \pi }
(
π
,
2
π
)
{\displaystyle (\pi ,2\pi )}
2
π
{\displaystyle 2\pi \,}
度
0
∘
{\displaystyle 0^{\circ }}
(
0
∘
,
90
∘
)
{\displaystyle (0^{\circ },90^{\circ })}
90
∘
{\displaystyle 90^{\circ }}
(
90
∘
,
180
∘
)
{\displaystyle (90^{\circ },180^{\circ })}
180
∘
{\displaystyle 180^{\circ }}
(
180
∘
,
360
∘
)
{\displaystyle (180^{\circ },360^{\circ })}
360
∘
{\displaystyle 360^{\circ }}
令x為該角度數。
有三種特殊角的組合,其度數和均為特殊的值:
餘角 :當兩個角的度數之和等於90°,即一個直角 ,這兩個角便是餘角。若兩個相鄰的角互為餘角,兩個非共用邊會形成直角。在欧几里得几何 中,非直角的兩角即互為餘角。若角A 和B 互為餘角,以下的數學式會成立:
sin
2
A
+
sin
2
B
=
1
cos
2
A
+
cos
2
B
=
1
tan
A
=
cot
B
sec
A
=
csc
B
.
{\displaystyle {\begin{aligned}\sin ^{2}A+\sin ^{2}B&=1\\\cos ^{2}A+\cos ^{2}B&=1\\\tan A&=\cot B\\\sec A&=\csc B\end{aligned}}.}
(一角的正切 等於其餘角的餘切 ,一角的正割 等於其餘角的餘割 )
三角函數中的餘函數 ,其前綴「co-」就是餘角的意思。 補角 :當兩個角的度數之和等於180°,即一個平角 ,這兩個角便是互補角。若兩個相鄰的角互為餘角,兩個非共用邊會形成一直線。不過兩個不相鄰的角也可以是補角,例如平行四邊形中,任兩鄰角為互補角。圆内接四边形 的對角也是互補角。若點P為圓O外的一點,而過點P作圓的切線,切點分別在點T和點Q,則∠TPQ和∠TOQ為互補角。
兩互補角的正弦相等,其餘弦及正切(若有定義義)大小相等,但符號異號。
在欧几里得几何中,三角形兩角的和為第三角的補角。 explementary angles or conjugate angles. 當兩個角的度數之和等於360°
互為餘角的角a 和角b 圖中的銳角和鈍角形成一組互補角
同頂角
a
+
b
+
c
=
360
∘
{\displaystyle a+b+c=360^{\circ }}
直線上的鄰角
a
+
b
+
c
=
180
∘
{\displaystyle a+b+c=180^{\circ }}
與平行線有關的定理 當
A
E
{\displaystyle AE}
B
D
{\displaystyle BD}
a
=
c
{\displaystyle a=c}
同位角 ,
A
E
/
/
B
D
{\displaystyle AE//BD}
b
=
d
{\displaystyle b=d}
內錯角 ,
A
E
/
/
B
D
{\displaystyle AE//BD}
b
+
c
=
180
∘
{\displaystyle b+c=180^{\circ }}
同旁內角 ,
A
E
/
/
B
D
{\displaystyle AE//BD}
由角度的關係也可以推得兩直線平行
當
a
=
c
{\displaystyle a=c}
A
E
{\displaystyle AE}
B
D
{\displaystyle BD}
當
b
=
d
{\displaystyle b=d}
A
E
{\displaystyle AE}
B
D
{\displaystyle BD}
當
b
+
c
=
180
∘
{\displaystyle b+c=180^{\circ }}
A
E
{\displaystyle AE}
B
D
{\displaystyle BD}
二曲線在P點的夾角定義為二曲線在P點切線A 和B 的夾角 曲線和直線的夾角或是二曲線間的夾角定義為二曲線在交點處切線 的夾角。
在欧几里得空间 中,二個向量 u 及v 的角和其點積 及向量的長度有關:
u
⋅
v
=
cos
(
θ
)
‖
u
‖
‖
v
‖
.
{\displaystyle \mathbf {u} \cdot \mathbf {v} =\cos(\theta )\ \|\mathbf {u} \|\ \|\mathbf {v} \|.}
依上式可以用二個平面(或曲面)的法向量 ,計算二者之間的夾角,也可以根據二歪斜線 的向量計算其夾角。
在一個抽象的實數内积空间 中,在定義角時可以用內積
⟨
⋅
,
⋅
⟩
{\displaystyle \langle \cdot ,\cdot \rangle }
· ):
⟨
u
,
v
⟩
=
cos
(
θ
)
‖
u
‖
‖
v
‖
.
{\displaystyle \langle \mathbf {u} ,\mathbf {v} \rangle =\cos(\theta )\ \|\mathbf {u} \|\ \|\mathbf {v} \|.}
在複數的内积空间中,為了使餘弦的數值仍維持實數,因此需修改為
Re
(
⟨
u
,
v
⟩
)
=
cos
(
θ
)
‖
u
‖
‖
v
‖
.
{\displaystyle \operatorname {Re} (\langle \mathbf {u} ,\mathbf {v} \rangle )=\cos(\theta )\ \|\mathbf {u} \|\ \|\mathbf {v} \|.}
或者使用絕對值的標示:
|
⟨
u
,
v
⟩
|
=
cos
(
θ
)
‖
u
‖
‖
v
‖
.
{\displaystyle |\langle \mathbf {u} ,\mathbf {v} \rangle |=\cos(\theta )\ \|\mathbf {u} \|\ \|\mathbf {v} \|.}
後者不考慮向量的方向,因此是描述由向量
u
{\displaystyle \mathbf {u} }
v
{\displaystyle \mathbf {v} }
子空間
span
(
u
)
{\displaystyle \operatorname {span} (\mathbf {u} )}
span
(
v
)
{\displaystyle \operatorname {span} (\mathbf {v} )}
在黎曼几何 中,利用度量张量 來定義二條切線 之間的夾角,其中U 及V 是切線向量,g ij G 的分量。
cos
θ
=
g
i
j
U
i
V
j
|
g
i
j
U
i
U
j
|
|
g
i
j
V
i
V
j
|
.
{\displaystyle \cos \theta ={\frac {g_{ij}U^{i}V^{j}}{\sqrt {\left|g_{ij}U^{i}U^{j}\right|\left|g_{ij}V^{i}V^{j}\right|}}}.}
以地理 的觀點,地球上任何一個位置都可以用地理座標系統 來表示,此系統標示位置的經度 及緯度 ,兩者都以此點連至地球球心連線的角度來表示,經度是以格林威治子午線 為參考基準,而緯度是以赤道 為參考基準。
在天文學 中,天球 的一點可以用任何一種天球坐标系统 來表示,不過其基準則因坐标系统不同而不同。天文學量測二顆星星的角距離 時,會假想分別有二顆星星分別和地球 連成的直線,再量測這二條直線的夾角,即為角距離。
天文學家也會用角直徑 量測一物體的表觀大小。例如滿月 的角直徑約為0.5°。小角公式 可以將上述的角測量轉換為距離和大小的比值。
线性(平动)的量
角度(转动)的量
量纲
—
L
L2
量纲
—
—
—
T
时间 : t s 位移积分 : A m s T
时间 : t s
—
距离 : d 位矢 : r s x 位移 m 面积 : A m2 —
角度 : θ 角移 : θ rad 立體角 : Ω rad2 , sr
T−1
頻率 : f s−1 Hz 速率 : v 速度 : v m s−1 面積速率 : ν m2 s−1 T−1
頻率 : f s−1 Hz 角速率 : ω 角速度 : ω rad s−1
T−2
加速度 : a m s−2 T−2
角加速度 : α s−2
T−3
加加速度 : j −3 T−3
角加加速度 : ζ s−3
M
质量 : m kg ML2
轉動慣量 : I m2
MT−1
动量 : p 冲量 : J m s−1 , N s 作用量 : 𝒮 actergy : ℵ m2 s−1 , J s ML2 T−1
角动量 : L 角衝量 : ι m2 s−1 作用量 : 𝒮 actergy : ℵ m2 s−1 , J s
MT−2
力 : F 重量 : F g kg m s−2 , N 能量 : E 功 : W kg m2 s−2 , J ML2 T−2
力矩 : τ moment M kg m2 s−2 , N m 能量 : E 功 : W kg m2 s−2 , J
MT−3
加力 : Y kg m s−3 , N s−1 功率 : P kg m2 s−3 , W ML2 T−3
rotatum P kg m2 s−3 , N m s−1 功率 : P kg m2 s−3 , W